Encontre o campo elétrico a uma distância acima do centro de um disco circular plano de raio (Figura 2.10), que tem uma densidade superficial de carga uniforme . O que a sua fórmula revela no limite ? Verifique também para o caso .
Passo 1
Falaaa, tudo belezaa?? Para simplificarmos este exercício vamos usar a resposta do Problema 2.5, onde encontrarmos o campo elétrico para o contorno do disco. Bora lá!!!
Passo 2
Os parâmetros do exercício podem ser analisados na figura abaixo:
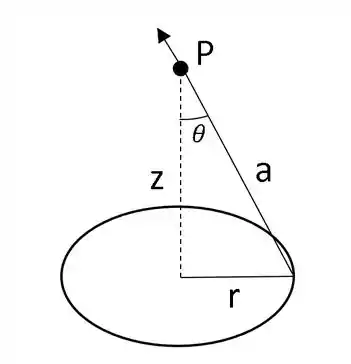
O resultado que encontramos para o contorno do disco foi o seguinte:
Portanto, o disco completo será o campo elétrico acima integrado da origem até o raio do disco em relação a .
Quando o segundo termo do parêntese irá tender a zero e o campo elétrico será:
E quando for muito maior do que poderemos desconsiderar o primeiro termo e o campo elétrico se resumirá a: