Encontre o campo elétrico (magnitude, direção e sentido) a uma distância acima do ponto central entre duas cargas iguais, , que estão separadas por uma distância (Figura 2.4). Verifique se o resultando é coerente com o com se espera quando .
(b) Repita a parte (a), só que desta vez faça a carga do lado direito igual a em vez de .
Passo 1
Falaaa, tudo bemm?? Neste exercício vamos usar a fórmula geral do campo elétrico entre duas cargas:
Porém, para resolvermos a questão, vamos fazer algumas interpretações da figura abaixo.
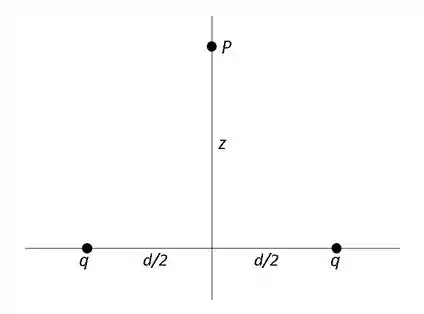
Passo 2
Para a primeira parte da questão, as duas cargas são positivas e queremos saber qual é o campo elétrico que as duas exercem no ponto .
Como as duas cargas são positivas e estão de forma simétrica no exemplo, a componente horizontal do campo elétrico irá se cancelar no ponto que estamos analisando. Portanto, como a análise é bidimensional, o campo elétrico será apenas na direção vertical.
Na direção vertical temos que o campo elétrico no ponto é dado por:
Os parâmetros podem ser analisados na figura abaixo:
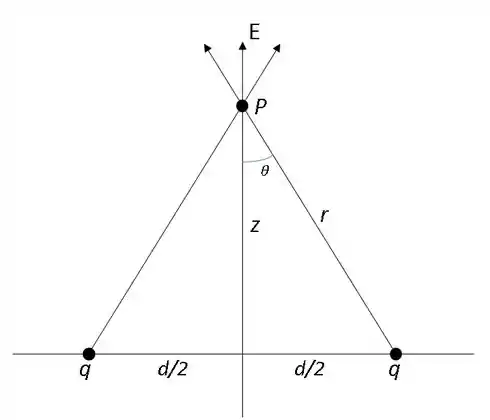
Como as cargas e o ponto formam um triângulo retângulo. A distância que cada uma das cargas está do ponto é definida pela soma dos quadrados dos catetos:
E o pode ser escrito como cateto adjacente sobre hipotenusa.
Substituindo os valores na fórmula do campo elétrico.
Neste caso, se o for muito maior que . Então, poderemos desprezar da fórmula, e o campo elétrico se reduzirá a:
Passo 3
Nesta segunda parte da questão, o vetor que será cancelado será o vertical. E a componente horizontal é dada como:
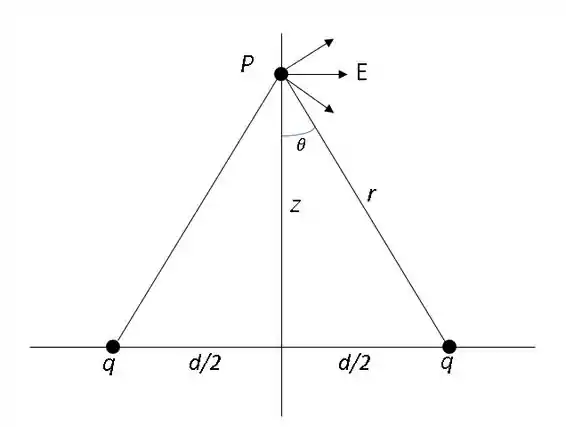
Considerando as substituições do passo 2, mas agora o seno é cateto oposto sobre hipotenusa:
Então, o campo elétrico é:
Nesta parte, se o for muito maior que . Poderemos desprezar , e a fórmula poderá ser considerada como: