a) Encontre as expressões matemática para e após a chave ser fechada na figura 12.77
b) Determine e em
Passo 1
Salve salveeee, vamos lá! Temos esse circuito aqui olha:
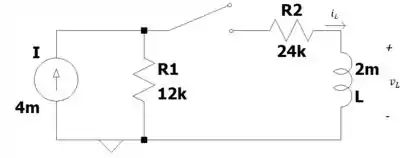
Vamos simplificar isso aí quando a chave é fechada hehe como temos uma fonte de corrente em paralelo com um resistor, podemos fazer a conversão para uma fonte de tensão em série com esse mesmo resistor, sendo que a fonte vai ter tensão de
Então, podemos deixar o circuito assim:
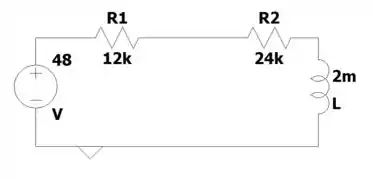
Agora simmm, nosso circuito ta bonitinho pra trabalharmos com ele :D
Passo 2
a) A primeiríssima coisa do mundo que precisamos fazer para encontrarmos as expressões é calcular o valor de . Ele vai ser:
Então
Passo 3
Boaa, agora que temos o podemos encontrar as expressões que queremos. Para , vamos usar
Substituindo os valores:
Então a expressão de é
Passo 4
Para , podemos usar
Substituindo os valores, temos a expressão de
Passo 5
b) Agora é só a gente usar as expressões do item anterior substituindo
Primeiro para :
Então:
Passo 6
Agora para :
Então
E acabaaaamosss
Resposta
a)
b)