A Equação 9.36 descreve a onda em uma corda linearmente polarizada mais generalizada. Polarização linear (ou ‘plana’) (assim chamada porque o deslocamento é paralelo a um vetor fixo ) resulta da combinação de ondas horizontalmente e verticalmente polarizadas, de mesma fase (Equação 9.39). Se os dois componentes são de mesma amplitude, mas fora de fase por (digamos, , ), o resultado é uma onda circularmente polarizada. Nesse caso:
(a) Em um ponto fixo , mostre que a corda se move em círculo em torno do eixo . Seu movimento é no sentido horário ou anti-horário quando você olha ao longo do eixo em direção à origem? Como você criaria uma onda que circulasse no outro sentido? (Em ótica, o caso horário é chamado de polarização circular à direita, e o anti-horário, de polarização circular a esquerda.)
(b) Desenhe a corda no tempo .
(c) Como você agitaria a corda a fim de produzir uma onda circularmente polarizada?
Passo 1
Falaaa, meu querido/minha querida!!! Para resolvermos essa questão, precisamos saber que para uma onda linearmente polarizada, o deslocamento das partículas da corda é dado por:
Agora, para resolvermos a questão, precisamos manipular as equações acima com as condições que o enunciado nos deu. Bora lá!!!
Passo 2
Antes de tudo, para definirmos se o movimento tem sentido horário ou anti-horário, vamos encontrar a onda circularmente polarizada. Para isso, adicionamos a fase na componente .
Supondo que a gente está observando a partícula em , a trajetória dela é dada por:
Logo, a trajetória é um círculo. Sendo uma onda polarizada no sentido horário, uma vez que, se então:
Nesse ponto, quando cresce, a componente inicialmente diminui e a componente cresce negativamente, de modo que a polarização é no sentido horário.
Passo 3
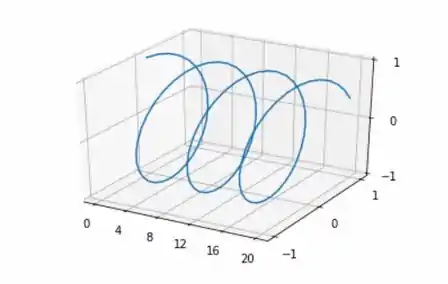
Passo 4
Para obter um movimento circular, basta agitar a corda de forma circular, pois qualquer movimento no início da corda será replicado no resto da corda.
Resposta
Resolução nos passos anteriores.