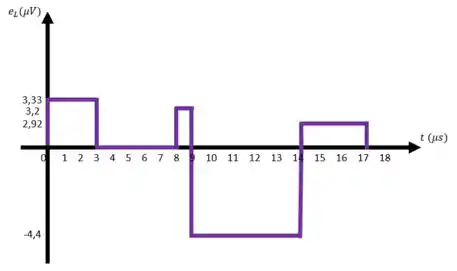
Esboce a forma de onda para a tensão induzida em um indutor de se a corrente no indutor variar de acordo com o gráfico visto na figura 12.67
Passo 1
E aííí, tudo certinho?
Olha, a equação primordial pra esse exercício é essa aqui:
E o segredo aqui basicamente é ir variando o valor de de acordo com o gráfico dado pelo enunciado, lembrando que
Mas quem é ???
Lembrando do conceito de derivada, vai ser a inclinação da reta em cada intervalo, então vamos lá??
Passo 2
O primeiro intervalo que temos no gráfico do enunciado é de a
Nesse intervalo, temos
Então:
Nesse intervalo, a reta da corrente é constante. Ou seja: sua inclinação vale 0
Vamos lá para os próximos intervalos
Passo 3
Nesse intervalo, temos
Então:
Aqui temos
Então
Aqui temos
Então
Boaaaa, agora é só esboçarmos o gráfico pra cada intervalo :P
Passo 4
Esboçando os resultados que temos em cada intervalo, nosso gráfico fica assim:
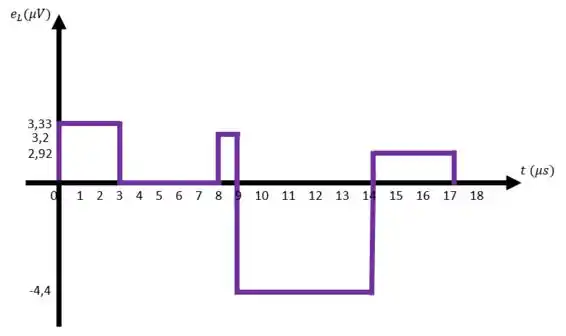
E é isssooo meu povo
Resposta