Esboce o gráfico das seguintes formas de onda:
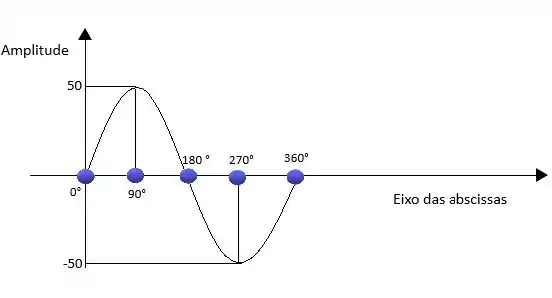
- 50 sen (ωt + 0°)
- -20 sen (ωt + 2°)
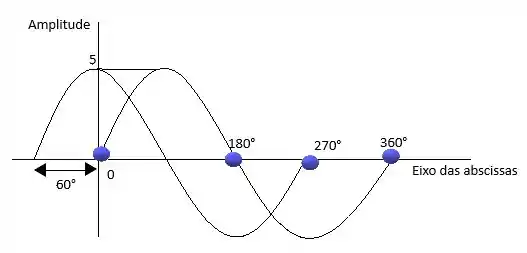
- 5sen (ωt + 60°)
- 4 cos ωt
- 2 cos (ωt + 10°)
- -5 cos (ωt + 20°)
Passo 1
Saudações galerinha! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Pra te lembrar ainda mais vou te mostrar o gráfico da função senoidal coma expressão geral (1) acima.
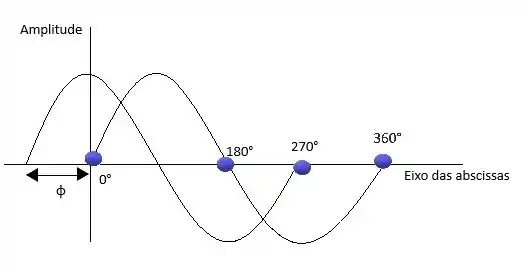
Neste caso os ângulos estão em graus
Bora começar então resolver nossa questão.
- Primeiro vamos substituir o ângulo de defasagem e repetimos os ângulos em graus.
- Agora vamos fazer a mesma coisa do passo anterior, mas com calma pois se observamos bem a amplitude aparentemente está negativa. Este sinal está associado a função seno e não a amplitude. Então podemos reescreve-la assim:
Se observamos direitinho o ângulo de defasagem é 0 ° logo a senóide começará no ângulo de 0° ficando na forma de gráfico abaixo.
Passo 2
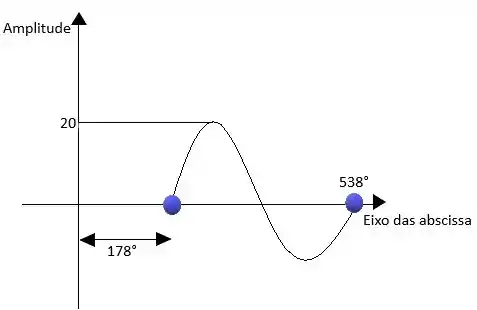
-20 sen (ωt + 2°)
20 [- sen (ωt + 2°)]
Como a função seno é ímpar podemos escrever:
20 sen (ωt + 2°- 180°)
20 sen (ωt – 178°)
O sinal negativo do argumento da função seno, significa que a função está adiantada, logo seu gráfico será:
Passo 2
(c) Agora vamos fazer a mesma coisa do passo anterior, mais o ângulo e defasagem não será mais 0° e sim 60°, então vamos só substituir no gráfico da expressão geral.
O gráfico ficará sim.
Passo 3
(d) Nesta alternativa temos uma pequena diferença pois a função está escrita em função do cosseno e não do seno.
Mais relaxa, essa situação é fácil de resolver!
Vale só lembrar que
Rescrevo o a função em termo do seno teremos:
Para o gráfico esse + 90° significa que a função está atrasada 90°, logo seu gráfico será:
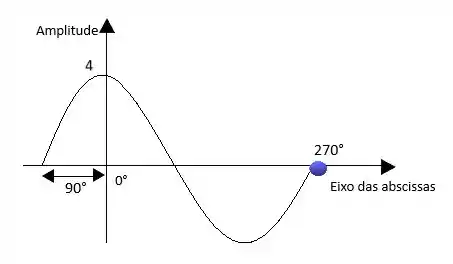
Passo 4
Quase acabando!

(e) Mais uma vez nessa questão a função não está expressa em função do seno, logo temos que reescreve-la utilizando:
Bora lá então
Devo somar 90° para transformá-la em função seno.
Ou seja a função que vamos esboçar está atrasada100°
Seu gráfico ficará assim!
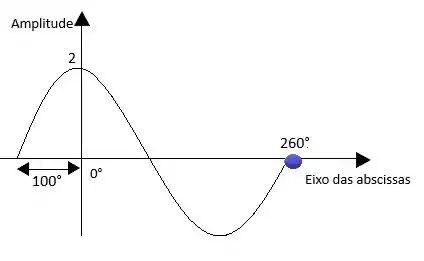
Ei! De onde veio esse 260°
Ele apareceu com a subtração de 360° - 100° = 260°, responsável por forma 1 ciclo a função senoidal.
Passo 5
Última, UFA!
Nessa última temos a união de dois problemas
1º a função não está escrita como função senoidal
2º a amplitude está negativa
E AGORA! Relaxa
Dividir para conquistar
Vamos primeiro escrever a função cosseno como seno, para isso vamos utilizar a identidade
Aplicando em nossa alternativa, teremos:
Prontinho! Primeiro problema resolvido, nossa função agora é:
Agora vamos eliminar esse sinal negativo da amplitude.
UFA!
Vamos agora esboçar nosso gráfico, lembrando que esse sinal negativo significa que a função está adiantada 70 °.
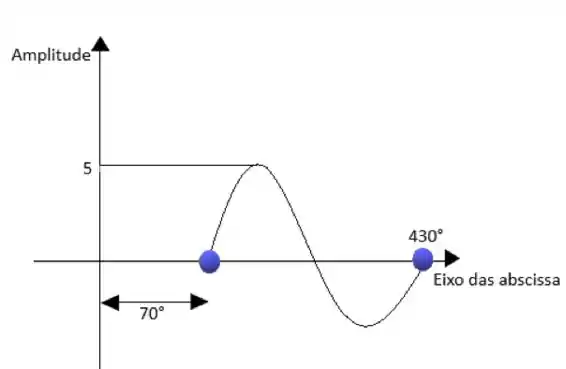
Acabamos por aqui, vamos para próxima?
Te vejo lá!
Resposta
Ei, a resposta está no passo a passo :)