Esboce o gráfico de sen ( 377t + 60°) usando como unidade do eixo das abscissas:
- O ângulo em graus
- O ângulo em radianos
- O tempo em segundos
Passo 1
Oi galerinha! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Pra te lembrar ainda mais vou te mostrar o gráfico da função senoidal coma expressão geral (1) acima.
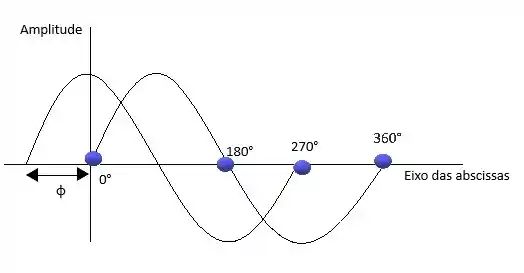
Neste caso os ângulos estão em graus
Bora começar então resolver nossa questão.
Primeiro vamos substituir do ângulo de defasagem e repetimos os ângulos em graus.
Ei! Não podemos esquecer que em nossa questão a amplitude não aparece explicitamente o que significa que é 1
Esboçando nosso gráfico teremos:
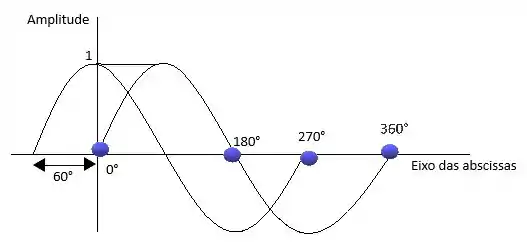
Passo 2
Agora vamos fazer a mesma coisa do passo anterior, mais os ângulos devem estar em radianos.
Lembra passar de grau para radianos?
Sem problema, vamos relembrar.
Então vamos transformar os ângulos 0°, 90°, 180°,270° e 360° em radianos.
Lembrando que essa transformação faz por regra de três beleza
Bora começar então.
Radiano Grau
π ------------------- 180°
X -------------------- 0°
Aplicando meio por extremos, teremos:
x.180 =
X =
X= 0°
Bora fazer para os ouros ângulos?
Radiano Grau
π ------------------- 180°
X -------------------- 180°
Aplicando meio por extremos, teremos:
x.180 =
X =
X = π
Radiano Grau
π ------------------- 180°
X -------------------- 270°
Aplicando meio por extremos, teremos:
x.180 =
X =
X =
Radiano Grau
π ------------------- 180°
X -------------------- 360°
Aplicando meio por extremos, teremos:
x.180 =
X =
X =
Ufa! quase terminando
Falta a última transformação que é o ângulo de fase.
Radiano Grau
π ------------------- 180°
X -------------------- 60°
Aplicando meio por extremos, teremos:
x.180 =
X =
X =
Vamos só montar nosso gráfico, substituindo os valores de grau para radiano.
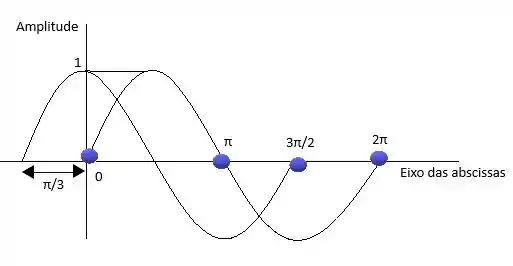
Passo 3
(c) Para nossa última alternativa vamos ter que transformar esses ângulos em segundos utilizando a formula da frequência angular
Onde ω= 377
Bora lá então!
0° -> t= = 0 s
360° -> t= = 16,6 ms
180° -> t= = 8,33 ms
90° -> t= = 4,15 ms
270° -> 8,33 + 4,15 = 12,48 ms
Não podemos esquecer de encontrar o tempo em segundo do ângulo de defasagem
Para isso vamos fazer uma pequena regrinha de três
Ângulo período
90-------------------4,15 ms
60 -------------------------x
Aplicando Meio por extremo
90.x = 4,15 . 60
90 x = 249
X=
X =2,76 ms segundos
Prontinhos !!
Agora vamos substituir os ângulos para o tempo em segundos.
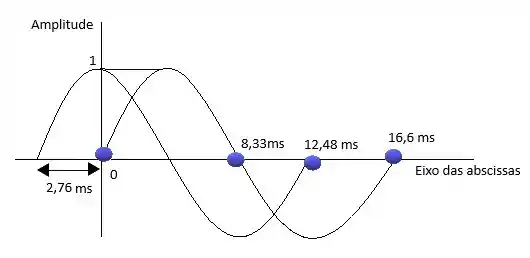
Terminamos vamos para a próxima questão?
Resposta
Ei, a resposta está no passo a passo :)