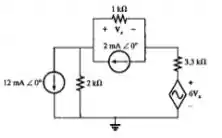
Escreva as equações nodais do circuito visto na Figura 17.77 e determine a tensão no resistor de 2k ohms.
Passo 1
Faaala, galerinha!! Bora resolver juntos essa questão??
Bom, antes de tudo, vamos resolver a letra a lembrando que os valores contidos nela são:
Prontinho! Agora, vamos pensar juntos aqui nos arranjos presentes nos nós.
Passo 2
Aqui, precisamos lembrar das Leis de Kirchoff e aplicá-las para encontrarmos as equações de V1 e V2. Vamos juntos lembrar um pouquinho: ela nos diz que a soma de todas as correntes que chegam em um nó do circuito é igual a soma da corrente que deixam esse mesmo nó. Sendo assim, podemos dizer que:
Logo, temos essa primeira equação:
Além disso, se partirmos do segundo nó, encontramos que
Passo 3
O mais difícil foi feito: entendemos as equações desse circuito e agora só resta substituir os valores e resolver as equações do sistema linear. Bora juntos??
Temos:
Substituindo V2 na primeira equação:
Continuando, podemos substituir os valores, e teremos que
Se resolvermos essa equação, encontraremos que
Passo 4
Voltando para a equação 2:
Como V1=-2,
Prontinho!! Resolvemos tudo, tendo que