- Escreva as equações nodais para o circuitos mostrados na Figura 8.115.
- Calcule as tensões nodais.
- Determine a intensidade e polaridade das tensões entre os terminais de todos os resistores.
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
-
- Vamos considerar a seguinte expressão para converter a fonte de tensão em fonte de corrente
Substituindo
Assim, o valor da fonte atual é 5A.
Passo 2
Vamos redesenhar o circuito
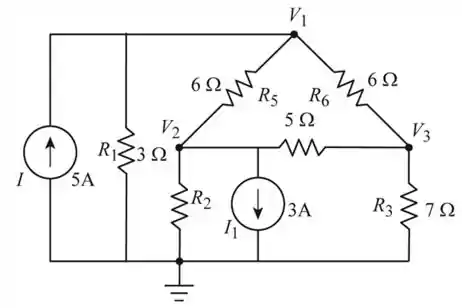
Passo 3
Vamos considerar o nó 1 na Figura acima, e encontraremos a tensão usando a análise nodal
Vamos considerar o nó 2 na Figura acima, e encontraremos a tensão usando a análise nodal
Vamos considerar o nó 3 na Figura acima, e encontraremos a tensão usando a análise nodal
Logo, a equação (1), equação (2), equação (3), são as equações nodais para esta rede dada.
Passo 4
- Vamos considerar a seguinte expressão para converter a fonte de tensão em fonte de corrente
Substituindo
Assim, o valor da fonte atual é 5ª.
Passo 2
Vamos redesenhar o circuito
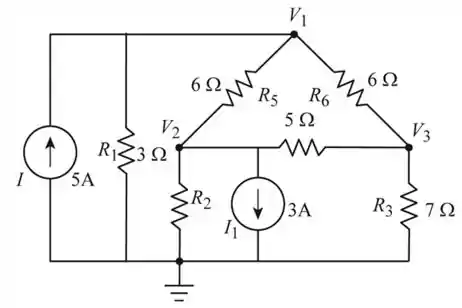
Passo 3
- Vamos considerar o nó 1 na Figura acima, e encontraremos a tensão usando a análise nodal
Vamos considerar o nó 2 na Figura acima, e encontraremos a tensão usando a análise nodal
Vamos considerar o nó 3 na Figura acima, e encontraremos a tensão usando a análise nodal
Logo, a equação (5), equação (6), equação (7), são as equações nodais para esta rede dada.
Resposta
Portanto, as equações nodais foram calculadas para esta rede.
Portanto, as equações nodais foram calculadas para esta rede.