- Escreva as equações nodais para os circuitos vistos na Figura 8.114.
- Calcule as tensões nodais.
- Determine as intensidades e polaridades das tensões entre os terminais de todos os resistores.
Passo 1
Alô Alô, galerinha do responde ai, borá la
-
- Vamos considerar a seguinte equação para converter a fonte de tensão em fonte de corrente
- Considerando a seguinte formação de matriz e encontrando os valores de tensão usando determinantes.
- Considerando a seguinte fórmula e encontraremos a tensão através da resistência .
Onde ,
é a fonte de tensão
é a resistência
Vamos fazer as substituições numéricas
Assim , o valor da fonte atual é
Passo 2
Vamos redesenhar a rede como mostrado a Figura 1.
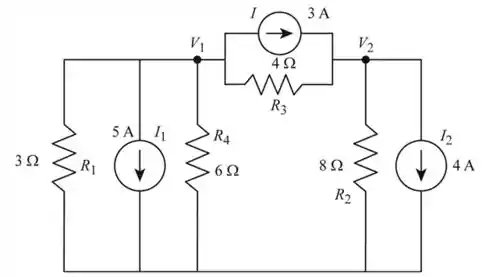
Passo 3
Consideremos o nó 1 na Figura 1, e encontraremos a tensão usando a análise nodal
Considere o nó 2 na Figura 1 e encontre a tensão usando a análise nodal.
Assim, a equação (2) e a equação (3) são as equações nodais para a rede elétrica.
Assim, as equações nodais são calculadas para a rede elétrica.
Passo 4
Partindo da equação (4), iremos encontrar os valores de tensão usando determinantes
Sendo assim, os valores de tensão, é .
Passo 5
Considerando a seguinte fórmula, iremos encontrar a tensão através da resistência
Assim, a tensão através dos valores de cada resistor foi calculada
Passo 6
A rede do circuito elétrico é mostrada na Figura 2
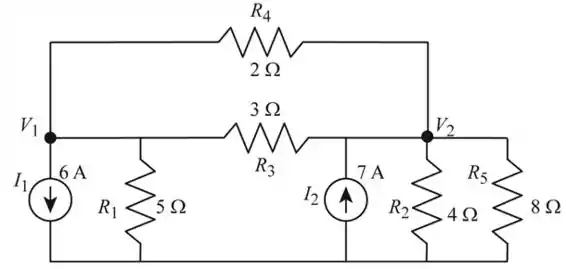
Passo 2
- Considere o nó 1 da Figura 2, e encontraremos a tensão usando análise nodal
- Considerando a seguinte formação de matriz e encontrando os valores de tensão usando determinantes.
- Considerando a seguinte fórmula e encontraremos a tensão através da resistência .
Considerando o nó 2 na Figura 2 e encontrando a tensão usando a análise nodal.
Assim, a equação (5) e a equação (6) são as equações nodais para a rede elétrica.
Assim, as equações nodais são calculadas para a rede elétrica.
Passo 8
Partindo da equação (4), iremos encontrar os valores de tensão usando determinantes
Sendo assim, os valores de tensão, é .
Passo 9
Considerando a seguinte fórmula, iremos encontrar a tensão através da resistência
Assim, a tensão através dos valores de cada resistor foi calculada
Resposta
- Verifique do passo 1 ao 5.
- Verifique do passo 6 ao 9.