(a) Escreva a matriz que descreve uma transformação de Galileu (Eq. 12.12).
(b) Escreva a matriz que descreve uma transformação de Lorentz ao longo do eixo y.
(c) Encontre a matriz que descreve uma transformação de Lorentz com velocidade v ao longo do eixo x seguido por uma transformação de Lorentz com velocidade ao longo do eixo y. Importa em que ordem as transformações são realizadas?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- A transformação de Galileu ao longo do eixo x é
- Agora as equações das transformações de Lorentz ao longo do eixo y é
- A matriz de transformação de Lorentz com velocidade v ao longo do eixo x é
Logo, a forma matricial, das equações acima podem ser descritas como:
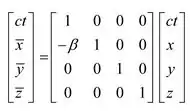
Passo 2
Portanto, sua forma matricial, com base nas equações a cima, ficará da seguinte maneira
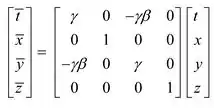
Passo 3
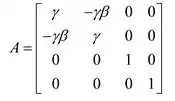
Agora a matriz de transformação de Lorentz com velocidade ao longo do eixo y é
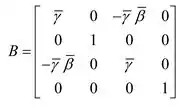
Portanto, como as matrizes , elas não comutam, por isso a ordem importa.
Resposta
Portanto, como as matrizes , elas não comutam, por isso a ordem importa.