Uma espira quadrada é recortada de uma folha grossa de alumínio. Ela é em seguida posicionada de forma que a sua parte superior esteja em um campo magnético uniforme B, e deixada em queda sob a ação da gravidade (Figura 7.19). (No diagrama, o sombreado indica a região do campo; B aponta para dentro da página). Se o campo magnético é 1T (um campo padrão em laboratórios), encontre a velocidade terminal da espira (em m/s). Encontre a velocidade da espira como função do tempo. Quanto tempo ela demora (em segundos) para alcançar, digamos, 90 por cento da velocidade terminal? O que aconteceria se você cortasse uma pequena fenda no anel, interrompendo o circuito? [Observação: o resultado não depende das dimensões da espira; determine os números de fato, nas unidades indicadas]
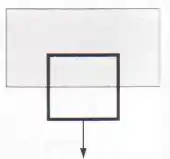
Figura 7.19
Passo 1
E aí galerinha, neste problema vamos relembrar alguns conceitos da mecânica. O primeiro ponto neste problema é determinar a velocidade terminal da espira. Da mesma forma que fazíamos na mecânica, precisamos descrever as forças que atuam sobre a espira.
- Força peso – representação da atuação gravitacional sobre a espira.
- Força magnética- representação da atuação do campo magnético sobre a espira.
A força peso é expressa por:
Onde m é a massa da espira e g a aceleração da gravidade. Já a força magnética ascendente neste caso, é expressa por:
Podemos encontrar uma expressão para a corrente em função das variáveis conhecidas. Utilizando a lei de Ohm, temos:
Inserindo a expressão acima na equação da força magnética, temos:
Que resulta em:
Passo 2
Para encontrar a velocidade terminal, temos que fazer uso da segunda lei de Newton:
A força “resistiva” neste caso, será a força magnética.
dividindo todos os termos pela massa, temos:
como B, l, m e R são constantes, podemos adotar , assim temos:
quando chegamos a um regime onde o sistema atinge a velocidade terminal, esse movimento não é mais um movimento acelerado, logo , que nos resta:
assim,
Retornado as variáveis que conhecemos, teremos:
Passo 3
O segundo ponto desse problema, nos pede para encontrar a velocidade da espira em função do tempo. Para isso, podemos utilizar a equação construída no passo anterior para dar a partida:
sendo , podemos reescrever a equação como:
podemos separar os integrantes em ambos os lados da equação:
Integrando ambos os lados, teremos:
O que temos que fazer agora, se resume a álgebra, pois temos que isolar o . Com isso teremos:
sendo , definido como velocidade terminal, podemos escrever a velocidade em função do tempo como:
Passo 4
Agora temos que descobrir, quanto tempo demora para a espira atingir 90% da velocidade terminal. Se queremos o tempo, a equação que vamos utilizar é a da velocidade dependente do tempo (que escrevemos no passo anterior). Os 90% da velocidade terminal, corresponderá:
Então,
Precisamos isolar o t da equação acima, que irá resultar em:
Passo 5
O que aconteceria se você cortasse uma pequena fenda no anel, interrompendo o circuito?
Uma das grandezas que essa condição afetaria, seria a massa, que agora seria expressa por:
onde é a densidade do alumínio e o restante da equação corresponde ao “novo volume” da espira. A resistência também seria afetada, pois está diretamente ligada as características espaciais do condutor (segunda lei de Ohm).
Sendo a condutividade do alumínio. Então, como esse corte na espira gera mudanças na massa e na resistência, termos que reestruturar as equações da velocidade e do tempo t para 90% de .
Reorganizando esta equação, obtemos:
Que numericamente assume o valor:
E , assumirá a forma:
Resposta
Para o caso da espira completa:
Para o caso do corte na espira:
;