Em um experimento de aniquilação de par, um eletron (de massa m) com momento , atingiu um pósitron (com a mesma massa, mas carga oposta) em repouso. Eles se anquilam, produzindo dois fótons. (Por que eles não poderiam produzir apenas um fóton?) Se um dos fótons emerge a 60° da direção do eletron incidente, qual a sua energia?
Passo 1
Faaaaaala, galera... Tranquileba??
Temos que:
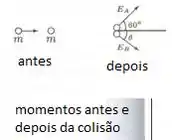
Para a conservação de energia:
Veja que a energia não depende da direção, o que já sabemos.
E o momento:
Na vertical:
Na horizontal:
Aqui já temos todas as informações para a resposta
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim, vamos elevar ao quadrado e adicioná-las
Ou
Passo 3
Vamos multiplicar e dividir por assim:
Assim: