As expressões a seguir se referem à corrente em uma reatância capacitiva de . Determine as expressões senoidais para a tensão em cada caso. Esboce as formas de onda de e no mesmo gráfico.
a)
b)
c)
d)
Passo 1
Viiiiixeee que parece difícil ein? Mas vem comigo aqui que é bem simples!! ;)
É só a gente pegar a amplitude da corrente de cada expressão e jogar na fórmula da Lei de Ohm (para o caso da reatância capacitiva, fazendo uma analogia a resistência elétrica). Dessa forma, a gente vai ter:
Aí com isso a gente descobre a amplitude da tensão e coloca na forma senoidal permanecendo a mesma frequência ;)
Mas é só isso??
Naaaoo!!!! É preciso levar em conta que a tensão no capacitor está atrasada em em relação à corrente que passa por ele!! Agora sim vamos lá!! ;)
Passo 2
Assim, temos que:
a)
Portanto, a expressão senoidal para a tensão fica:
Nesse sentindo, plotando as formas de onda de e no mesmo gráfico, temos:
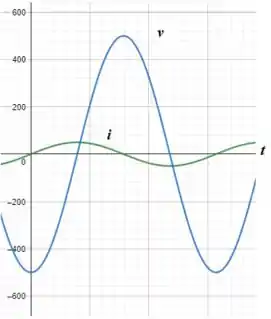
Passo 3
b)
Portanto, a expressão senoidal para a tensão fica:
Nesse sentindo, plotando as formas de onda de e no mesmo gráfico, temos:
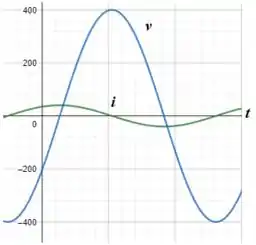
Passo 4
c) A gente sabe que:
Portanto, da expressão, temos:
Assim, fazendo a mesma coisa que fizemos nas letras anteriores, vemos que:
Portanto, a expressão senoidal para a tensão fica:
Nesse sentindo, plotando as formas de onda de e no mesmo gráfico, temos:
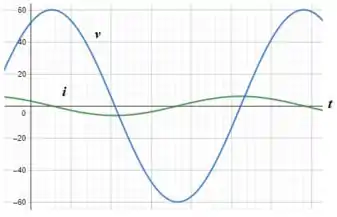
Passo 5
d) A gente sabe que:
Portanto, da expressão, temos:
Assim, fazendo a mesma coisa que fizemos nas letras anteriores, vemos que:
Portanto, a expressão senoidal para a tensão fica:
Nesse sentindo, plotando as formas de onda de e no mesmo gráfico, temos:
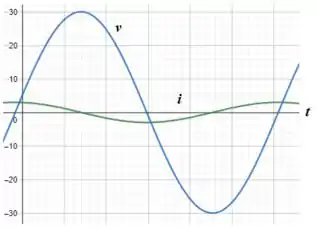
Resposta
a)
b)
c)
d)