As expressões a seguir representam a tensão num resistor de . Determine a expressão senoidal para a corrente. Além disso, esboce as formas de onda de e no mesmo gráfico.
a);
b);
c);
d).
Passo 1
Pela Lei de Ohm, sabemos que a queda de tensão em um resistor é dada por:
Dessa forma, basta analisar o valor máximo de cada função e dividir pela resistência (a qual é de )!!
Passo 2
Para a letra a), temos . Logo:
Logo, a expressão fica:
Plotando a expressão da tensão e da corrente num mesmo gráfico, temos:
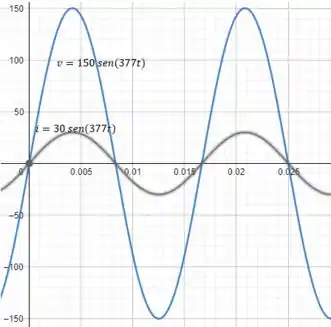
Passo 3
Para a letra b), temos . Logo:
Logo, a expressão fica:
Plotando a expressão da tensão e da corrente num mesmo gráfico, temos:
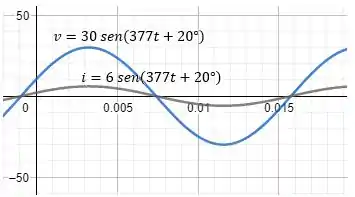
Passo 4
Para a letra c), temos . Sabemos que:
Portanto, a expressão de em termos de seno fica:
Assim, aplicando a Lei de Ohm:
Logo, a expressão fica:
Plotando a expressão da tensão e da corrente num mesmo gráfico (para um qualquer), temos:
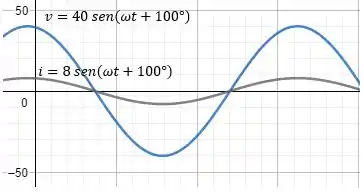
Passo 5
Para a letra a), temos . Mas antes, temos que:
Portanto, a expressão fica:
Logo, pela Lei de Ohm:
Logo, a expressão fica:
Plotando a expressão da tensão e da corrente num mesmo gráfico, temos:
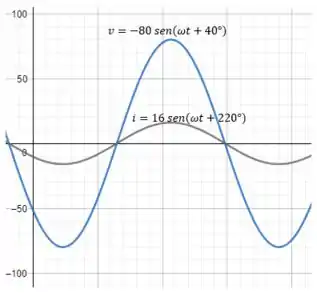
Resposta
a);
b);
c);
d).