Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Introdução a Análise de Circuitos, de Boylestad- Ed: 10º - Capítulo 13.Problemas - Ex. 21

Faça um esboço do gráfico da função -7,6 sen 43,6 t usando como unidade do eixo das abscissas:

  1. O ângulo em graus
  2. O ângulo em radiano
  3. O tempo em segundos.

Passo 1

Olá galera! tudo bem?

Antes de resolver essa questão, vamos só lembra a da função senóide:

A m sin ⁡ ω t               ( 1 )

Onde:

T é o período

A m é a amplitude da função

E também de seu gráfico

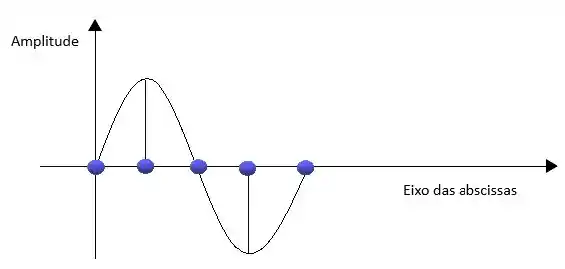
Observamos que a senóide mostrada acima é bem genérica, porque em nosso exercício vamos ter que completar as bolinhas azuis com ângulos em radiano, grau e tempo.

Lembrando também que devemos adicionar a amplitude em nosso gráfico.

Todos prontos?

Bora começar então.

  1. Usando a equação (1), e comparando com a função de nosso exercício teremos:

    2. A m sin ⁡ ω t             =   - 7,6   s e n 43,6 t

    Podemos observar que -7,6 ocupa o lugar de A m na função geral da senóide, logo a amplitude dessa função é -7,6 .

    Vamos esboçar nosso gráfico em graus. Ou seja nas bolinhas azuis devo colocar o ângulo em graus.

    Não esquecer que esses ângulos vem do ciclo trigonométrico, beleza!

    Prontinho, aí está nosso gráfico com os eixos das abscissas em grau.

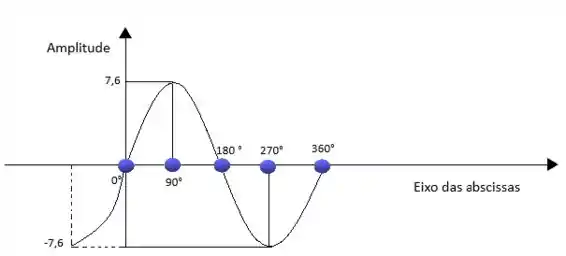
    O raciocino vai se repeti para todas as outras alternativas então, bora colocar a mão na massa e ficar fera nisso!

    Passo 2

  2. Usando a equação (1), e comparando com a função de nosso exercício teremos:

    3. A m sin ⁡ ω t             =   - 7,6   s e n   43,6 t

    Podemos observar que -7,6 ocupa o lugar de A m na função geral da senóide, logo a amplitude dessa função é -7,6.

    Vamos esboçar nosso gráfico em radianos. Ou seja nas bolinhas azuis devo colocar o ângulo em radianos

    Então vamos transformar os ângulos 0°, 90°, 180°,270° e 360° em radianos.

    Lembrando que essa transformação faz por regra de três beleza

    Bora começar então.

    Radiano Grau

    π ------------------- 180°

    X -------------------- 0°

    Aplicando meio por extremos, teremos:

    x.180 = π . 0 °

    X = 0 180

    X=0

    Bora fazer para os ouros ângulos?

    Radiano Grau

    π ------------------- 180°

    X -------------------- 90°

    Aplicando meio por extremos, teremos:

    x.180 = π . 90 °

    X = 90 . π 180

    X = π 2

    Radiano Grau

    π ------------------- 180°

    X -------------------- 180°

    Aplicando meio por extremos, teremos:

    x.180 = π . 180 °

    X = 180 . π 180

    X = π

    Radiano Grau

    π ------------------- 180°

    X -------------------- 270°

    Aplicando meio por extremos, teremos:

    x.180 = π . 270 °

    X = 270 . π 180

    X = 3 π 2

    Radiano Grau

    π ------------------- 180°

    X -------------------- 360°

    Aplicando meio por extremos, teremos:

    x.180 = π . 360 °

    X = 360 . π 180

    X = 2 π

    Ufa! quase terminando vamos só montar nosso gráfico, substituindo os valores de grau para radianos que encontramos.

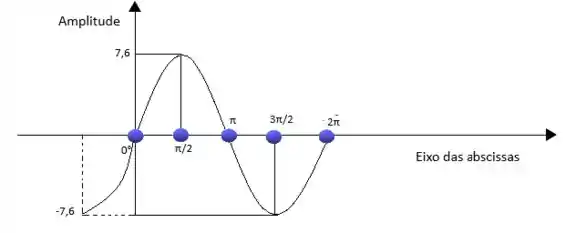
    Vamos para última, quase terminando!

    Passo 3

  3. Para nossa última alternativa vamos ter que transformar esses ângulos em segundos utilizando a formula da frequência angular

t = 2 π ω

Onde ω= 43,6

Bora lá então!

0° -> t= 2 .   0 43,6 = 0 s

360° -> t= 2 .   3,1415 43,6   = 144,1 ms

180° -> t= 144,1 2 = 72,05 ms

90° -> t= 144,1 4 = 36,02ms

270° -> 72,05 + 36,02 = 47,1 ms

Agora vamos substituir os ângulos para o tempo em segundos.

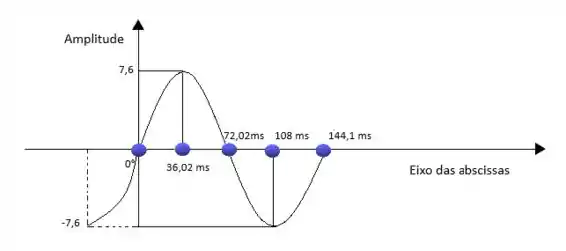
UFA!

Acabamos, te vejo no próximo exercício.

Resposta

Ei, a resposta está no passo a passo :)