Faça o gráfico da expressão a seguir em função do tempo para um período completo. Em seguida, determine a derivada da função usando a Equação (14.1) e plote um ciclo completo da derivada no mesmo gráfico que a função original. Compare o valor da derivada em vários pontos em função da inclinação da função senoidal original.
Passo 1
Opaa, bora primeiro plotar a função dada na questão para um período completo. Se liga como fica:
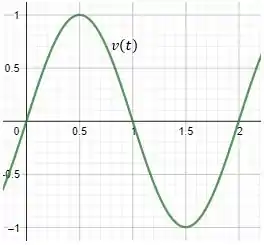
Passo 2
Da Equação 14.1 mencionada no enunciado, a gente tem que:
Dessa forma, aplicando a derivada na equação dada no enunciado, temos:
Plotando essa derivada no mesmo gráfico mostrado anteriormente, a gente vai ter:
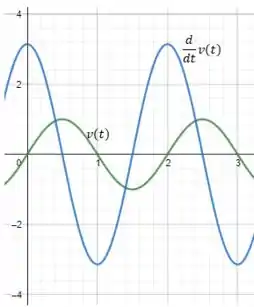
Se você analisar os pontos de máximo e mínimo da função , verão que v(t) será sempre zero. Entendeu não? Apoi se liga aqui, meu consagradx:
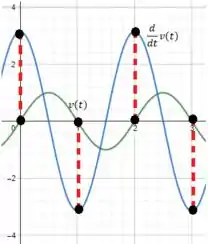
Agora sim, né? Facinho facinho ;)