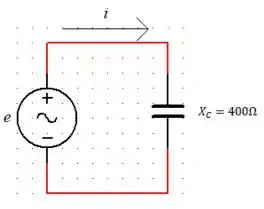
Na Figura abaixo, .
- Determine a tensão .
- Calcule o valor da capacitância em microfarads.
- Determine a dissipação média de potência no capacitor.
Passo 1
Se liga como é simples essa questão!
Pela Lei de Ohm para a reatância capacitiva, temos:
Em que e são a amplitude da tensão e da corrente, respectivamente.
Assim, temos que:
Agora é só jogar na expressão da tensão né? NÃÃÃOOOO
É preciso levar em conta que a corrente no capacitor está adiantada em em relação à corrente que passa por ele!!
Assim, temos que:
Passo 2
Sabemos que a reatância capacitiva é dada por:
Em que é a capacitância e é a frequência angular, a qual é dada por:
Assim, substituindo valores, temos que:
Passo 3
A potência dissipada é ZERO pois se trata de um capacitor!!
Mas se vc quer uma prova, vem cá!!
A gente sabe que a potência é dada por:
A gente sabe que a diferença de fase é de . Assim, seu cosseno é (zero), ocasionando em .
Agora sim B)