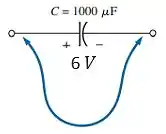
Figura do problema 25
Passo 1
Olá 😄, voltamos ao problema 25 novamente, mas sem o medo inicial 🤣.
Vamos anotar as informações do problema 25:
Processo de descarga, logo,
Anotar a resposta do problema 25:
Passo 2
Vamos dar início a nossa breve análise!
A equação da corrente fornecida pela seção 10.10 é escrita como:
A corrente é a corrente máxima, é a corrente instantânea, que será , todas essas são informações que temos. Só nos basta reorganizar a equação acima, para isolar o tempo (), que é o objetivo do problema.
Para tirar a exponencial do lado esquerdo, vamos aplicar o logaritmo em ambos os lados:
Arrumando um pouco melhor essa equação, podemos escrevê-la como:
Essa expressão também pode ser encontrada em exemplos resolvidos desta seção 😄.
Passo 3
Inserindo os valores na equação que encontramos, teremos:
Resposta
O tempo para que a corrente caia a metade de seu valor inicial é de: