Para o filtro de banda de atenuação visto na Figura 23.109:
- Determine
- Trace o gráfico da resposta em frequência de .
- Calcule para = 100 K e indique o efeito de sobre a curva do item (b).
- Repita o item (c) para
Passo 1
Saudações galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
a) Antes de começar teremos que lembrar de algumas relações que serão uteis na resolução desse exercício, beleza!
Para encontrar o ganho usaremos a relação:
Ei! A questão já lhe fornece
Vamos substituir os valores encontrado no circuito na relação acima:
Agora vamos precisar encontrar a impedância do filtro, lembra da fórmula?

Relaxa!
A fórmula é:
Substituindo os valores:
Quando o filtro esta´ em ressonância existe um ganho e uma tensão de saída, vamos calcula-los, tranquilo!
Para encontrar a relação do ganho com a tensão de saída, vou utilizar:
Aplicando nossos valores:
Logo o ganho será:
Utilizaremos a equação da frequência de corte encontrada no problema 30, beleza!
AFF! A equação pavorosa de novo!
Relaxa, vai ser tranquilo!
Olha ela aí
Utilizando as situações:
Substituindo na equação , teremos:
Criatura essa item não acaba não?

Tá quase acabando!
Agora devemos resolver essa pavorosa equação do 2º grau:
Para encontrar a largura da banda vamos utilizar a equação:
Em nosso exercício e , substituindo na equação acima:
Para encontrar , usarei a equação:
Ei! A questão já lhe fornece
Substituindo teremos:
Tudo bem? podemos continuar?
Vamos nessa então!
Passo 2
b) Para esse item devemos esboçar o gráfico. Só lembrando que nossa frequência de corte que podemos encontrar a relação entre e , utilizando a relação:
Aplicando os valores:
Traçando o gráfico, vamos obter:
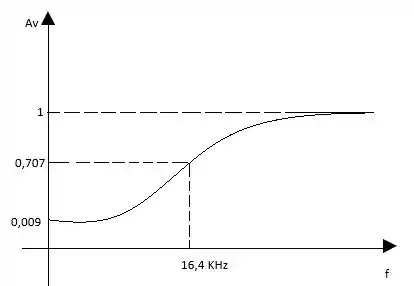
Passo 3
c) Se conectarmos uma carga a tensão de saída, deve ser calculando levando em consideração que terá um resistor de em paralelo com impedância já calculada anteriormente), ou seja temos que encontrar a resistência equivalente entre esses e depois substituir na fórmula da tensão de saída.
Tudo tranquilo aí?
Basta só lembrar que
Bora lá então!
Aplicando na equação de saída:
Aplicando nossos valores:
Para encontrar a relação da tensão de saída com o ganho, devo aplicar:
O que significa esse resultado?
Que a carga irá afeta a tensão de saída, à medida que a influência da impedância diminui para a resposta do circuito.
Que a carga afeta influência na tensão de saída
Passo 4
d) No último item temos que repeti o raciocínio anterior, mas agora o valor da carga mudará, beleza!
Se conectarmos uma carga a tensão de saída, deve ser calculando levando em consideração que terá um resistor de em paralelo com impedância já calculada anteriormente), ou seja temos que encontrar a resistência equivalente entre esses e depois substituir na fórmula da tensão de saída.
Tudo tranquilo aí?
Basta só lembrar que
Bora lá então!
Aplicando na equação de saída:
Aplicando nossos valores:
Para encontrar a relação da tensão de saída com o ganho, devo aplicar:
O que significa esse resultado?
Que a carga irá afeta minimamente a tensão de saída, à medida que a influência da impedância aumenta para a resposta do circuito. Por consequência da resposta a curva de ressonância ficara mais estreita e diminuir a largura da banda.
Ufa! Esse exercício chegou ao fim!
Vamos para o próximo
Resposta
a)
b)
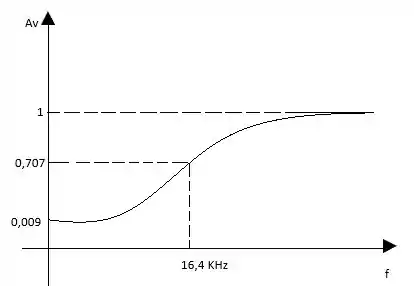
c) ; A carga influência na tensão de saída
d) ; A carga influência minimamente na tensão de saída