Para o filtro da Figura
a) Faça o gráfico em função da frequência usando o gráfico de Bode como referência.
b) Faça o gráfico de em função da frequência.
Passo 1
Olá galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
a) Nesta alternativa temos apenas que desenha um gráfico o gráfico de bode
Para isso é necessário encontrar as frequências, tranquilo!
Vamos começar então!
Sabemos que o ganho para esse circuito pode ser expresso por:
Para encontrar nossa primeira frequência , vou utilizar a relação:
Substituindo com os valores fornecidos no circuito:
Com a frequência de corte vamos usar a mesma relação:
Aplicando essas informações na equação do ganho teremos:
Prontinho! Vamos esboçar o gráfico agora?
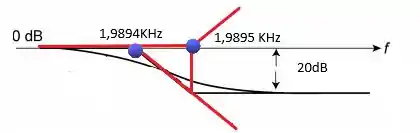
Até aí tudo beleza? vamos continuar então!
Passo 2
b) Por fim! Mas não menos importante último item.
Esboça a resposta da frequência para esse circuito, tranquilo né!
Só lembrando que
Para
Para
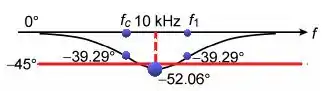
Aplicando nossas informações, nosso gráfico ficará assim.
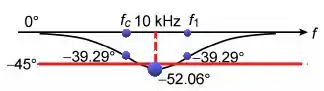
Bom galera, esse gráfico é bem simples com mais riquezas de você deve aumentar o eixo do X com diversas frequências e o eixo do Y com diversos ângulos.
Tranquilo?
Te vejo na próxima então!
Resposta
a)
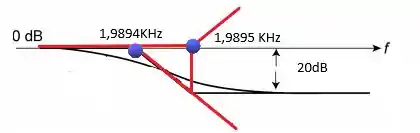
b)