Para o filtro R-C passa-baixa visto na figura 23.99:
a) Trace o gráfico de em função da frequência usando uma escala logarítmica para o eixo das frequências. Determine para e
b) Trace a curva da fase de em função da frequência, onde é o ângulo pelo qual está adiantada em relação a . Determine para e
Passo 1
Oiiii genteee
Olha só, a primeira coisa do mundo que precisamos saber nesse exercício é a frequência de corte , ela é calculada assim:
No circuito mostrado, temos e :
Agora sim, vamos lá!
Passo 2
Queremos traçar o gráfico de , que é calculado assim:
Substituindo :
Onde
Pronto, essa é a equação genérica que vamos usar para calcular o em e
Passo 3
Sabendo que , os valores de que vamos substituir na expressão de são
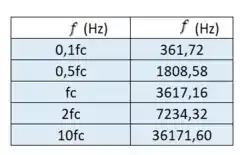
Então, substituindo esses valores de frequência na expressão , temos
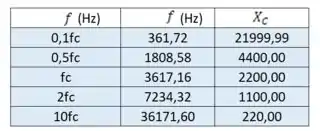
E, por fim, aplicando os dados que temos na expressão , encontramos os valores que vamos plotar:
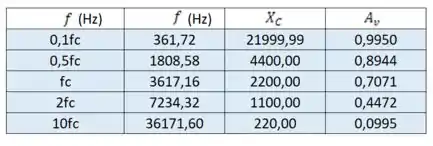
Passo 4
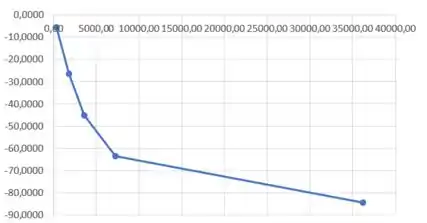
Plotando os dados da tabela anterior com escala logarítmica no eixo vertical, temos:
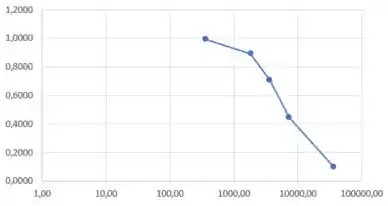
Passo 5
b) Agora vamos encontrar alguns valores de , que é calculado assim:
Onde
Nesse item, assim como no item anterior, vamos calcular para diferentes valores de frequência, que nos dão diferentes valores de :
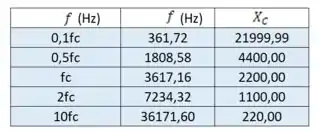
Substituindo esses valores na expressão , encontramos os valores de :
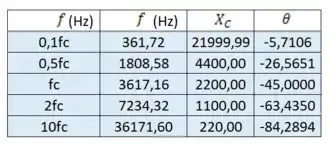
Vamos plotar isso em um gráfico comum:
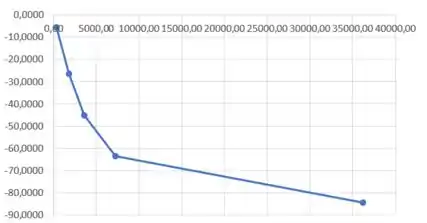
E acabamos galeraaa :D
Resposta
a) 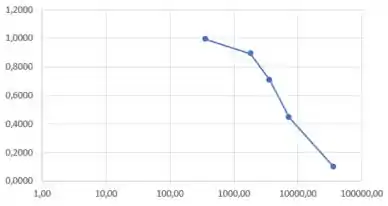
b)