Para o filtro passa-faixa visto na Figura 23.106:
- Determine
- Calcule e a largura da banda (BW) para
- Trace o gráfico de para a faixa de frequência de 1 kHz a 1 MHz.
- Calcule o módulo de para nas frequências de corte.
Passo 1
Saudações galera, tudo bem?
Vamos juntos resolver mais um exercício!
Antes de começar a resolver o primeiro item, vamos relembrar a equação utilizada para encontrar a frequência
Observamos a figura , temos lá o valor de L = e C= , substituindo na equação teremos:
Passo 2
Em nosso segundo item devemos encontrar para isso usaremos a relação:
Tudo tranquilo, vamos continuar então!
Lembrando que
Vamos substituir os valores encontrado no circuito na relação acima:
Para encontrar a largura da banda vamos utilizar a equação:
Substituindo teremos:
Eita, quase acabando!
Passo 3
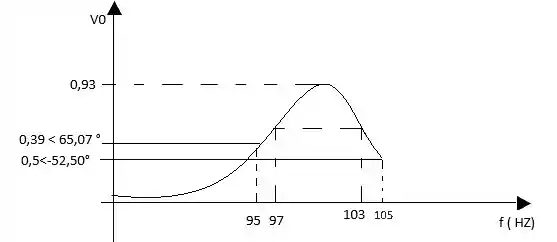
Esse item é o esboço do gráfico vai dá um trabalhinho, mas vamos conseguir juntos. Beleza!
Primeiro encontraremos utilizaremos a relação:
Substituindo os valores:
Segundo passo é calcular o ganho, lembra da fórmula?

Relaxa, sem problemas!
Usaremos
Aplicando nossos valores teremos:
Desde que
Vamos encontrar as frequências para traçar o gráfico, tranquilo!
Essas frequências calculadas são as limites no intervalo da curva de frequência.
Agora vamos encontrar a para algumas frequência dentro do intervalo:
Para teremos:
Quase acabando!
Para
Por fim, ao esboçar o gráfico teremos:
Passo 4
Quase acabando, último item:
Antes temos que lembrar como calculamos a tensão de saída nas frequências de corte, para isso utilizamos a relação:
Ou seja independe das frequências de corte a tensão permanece constante, vamos calcula-la então:
Prontinho, acabamos te vejo na próxima questão!
Resposta
a)
b);
c)
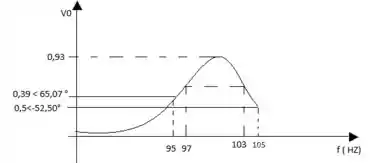
d)