Para o filtro passa-faixa visto na figura 23.105:
a) Trace o gráfico da resposta em frequência de usando uma escala logarítmica que se estenda de a
b) Qual é a largura de banda e a frequência central?
Passo 1
Falaaa galera!
A primeiríssima coisa que vamos fazer é calcular .
Como no caso temos um filtro passa faixa, vamos ter dois valores de , o do passa baixa e o do passa alta:
Agora simmm, vamos lá!
Passo 2
Então vamos lá fazer a análise do nosso filtro passa-faixa
Mas antes de tudo, vamos assumir que a impedância equivalente , ok? Pois o termo acaba sendo insignificante quando ta em paralelo com o hehehe
Então vamos lá calcular o em
Sabemos que
Beleza, aí pra esse caso temos que
Onde , então
Passo 3
Agora vamos calcular o em
Sabemos que
Beleza, aí pra esse caso temos que
Mas sabemos que , então
Passo 4
Agora vamos calcular na frequência intermediária entre as frequências de corte, que é onde devemos ter ganho máximo
Nesse caso, temos
E:
Entãooo:
Passo 5
Beleza, temos o , agora podemos encontrar o para essa faixa de frequência:
Então:
Que será o valor máximo no nosso gráfico
Passo 6
Fazendo os mesmos cálculos para outras frequências entre e , ou seja: calculando e , temos
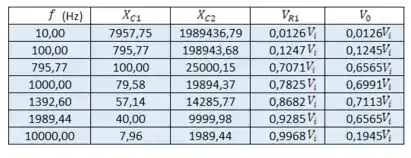
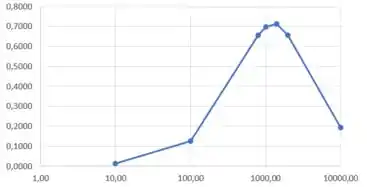
O que nos dá o gráfico de :
Passo 7
b) Para definirmos a largura de banda, vamos usar como parâmetro as frequências onde vale:
O que acontece em e
Então, a largura de banda é
Sendo que a frequência central vale:
Fechouuu?
Resposta
a) 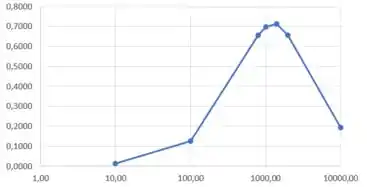
b)