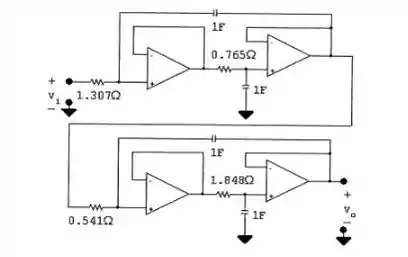
A finalidade deste problema é desenvolver as equações de projeto para o circuito na Figura P15.53. (Veja o Problema para sugestōes sobre o desenvolvimento de equações de projeto.)
a) Com base em uma análise qualitativa, descreva o tipo de filtro implementado pelo circuito.
b) Verifique a conclusão a que você chegou em (a) derivando a função de transferência . Escreva a funçāo de transferência na forma que a torne compatível com a Tabela 15.1.
c) Quantas escolhas livres há na seleção dos componentes do circuito?
d) Calcule as expressões para as condutâncias e em termos de e os coeficientes e . Veja o Problema para a definição de e )
e) Há restrições para ou ?
f) Suponha que o circuito na Figura P15.53 seja usado para projetar um filtro Butterworth passa baixas de quarta ordem de ganho unitário. Especifique os valores prototípicos de do filtro protótipo se, em cada seção de segunda ordem, forem usados capacitores de .
Passo 1
[a] Em baixas frequências as ramificações do capacitor estão abertas;. Em altas frequências, os ramos do capacitor são curtos-circuitos e a tensão de saída é zero. Portanto, o circuito se comporta como um filtro passa-baixa de ganho unitário.
Passo 2
[b] Seja a tensão-terra no terminal direito de . Observe que esta também será a tensão no terminal esquerdo de . As equações do domínios são
Ou
Que reduz para
Passo 3
[c] Existem quatro componentes do circuito e duas restrições impostas por H(s); portanto, há duas escolhas livres.
Passo 4
Passo 5
[e] Não, todos os capacitores fisicamente realizáveis produzirão resistores fisicamente realizáveis.
Passo 6
[f] Da Tabela 15.1 sabemos que a função de transferência do protótipo do filtro Butterworth de 4ª ordem é
Na primeira seção
Na segunda seção
Resposta
a. o circuito se comporta como um filtro passa-baixa de ganho unitário
b.
c. há duas escolhas livres.
d.
e. Não, todos os capacitores fisicamente realizáveis produzirão resistores fisicamente realizáveis.
f.