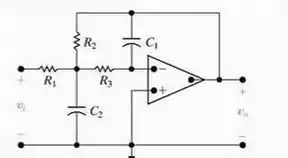
A finalidade deste problema é orientá-lo na análise necessária para estabelecer um procedimento de projeto para a determinação dos componentes de um filtro. O circuito a ser analisado é mostrado na Figura P15.48.
a) Analise o circuito do ponto de vista qualitativo convença-se de que o circuito é um filtro passabaixas com um ganho na faixa de passagem .b) Comprove sua análise qualitativa deduzindo a função de transferência . (Sugestāo: ao deduzir a função de transferência, represente os resistores por suas condutâncias equivalentes, isto é, e assim por diante.) Para usar a Tabela 15.1, coloque a função de transferência na forma
c) Agora, observe que temos cinco componentes de circuito e - e três restriçôes aplicadas à função de transferência - e À primeira vista, parece que temos duas opços livres entre os cinco componentes. Todavia, quando investigamos as relaçoes entre eles e as restriçōes à funçāo de transferência vemos que, se for escoIhido, há um limite superior para acima do qual não é possível obter um valor para . Com isso em mente, mostre que, se , as três condutâncias serão dadas pelas expressões
d) Com base nos resultados obtidos em (c), esboce o procedimento de projeto para selecionar os componentes do circuito, uma vez conhecidos ,
Passo 1
[a] Em frequências muito baixas, os dois ramos do capacitor estão abertos e, como o amplificador operacional é ideal, a corrente é zero. Portanto em baixas frequências o circuito se comporta como um amplificador inversor com ganho de. Em frequências muito altas, os ramos do capacitor são curtos-circuitos e, portanto, a tensão de saída é zero.
Passo 2
[b] Deixe o nó onde , e se unem ser denotado como a, então
ou
Resolvendo para
e
Passo 3
[c] equacionando coeficientes vemos que
Uma vez que pela hipótese
Resolvendo esta equação quadrática para , obtemos
Para que seja realizável
Passo 4
[d] 1. Selecione
2.Selecione tal que
3.Calcule
4.Calcule
5. Calcule
Resposta
tensão de saída é zero
b.
c.
d.