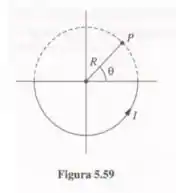
Por um fio semicircular passa uma corrente estacionária (ele deve estar ligado a alguns outros fios para completar o circuito, mas não vamos nos preocupar com eles aqui). Encontre o campo magnético no ponto no outro semicírculo (Figura 5.59).
[Resposta: ].
Passo 1
Olá pessoal, bora para mais uma!?
Vamos considerar um ponto no espelhado a P e chamá-lo de r’. Assim temos que:
E o ponto de estudo P, por comodidade chamamos de r. Assim temos:
Onde a distância entre r’ e r é expressa como:
E por último:
agora conseguimos calcular , assim :
Agora calculando o determinante, temos que:
Passo 2
Agora podemos calcular o campo magnético, assim temos:
Agora vamos colocar todas as constantes para fora da integral, para facilitar a visualização, assim temos:
Agora conseguimos reparar que dentro da integral temos elementos em cima e em baixo iguais, o que facilita um pouco. Assim temos:
A integral de cima é tabelada, com isso temos que:
E por fim, temos que:
Assim finalizamos mais uma! Até a próxima !!