Para a forma de onda vista na figura 24.56, determine:
a) O período
b) A largura
c) A frequência de repetição de pulsos
d) O valor médio
e) O valor eficaz
Passo 1
Olá galerinha, tudo bem?
Vamos começar a resolver mais um exercício, bora lá então!
(a) Observando o gráfico vamos focar nossos olhares para o eixo horizontal, para encontrar o período basta encontrar o tempo necessário para a forma de onda completa ciclo.
Se analisamos o gráfico percebemos que esse tempo corresponde a subtração de:
Passo 2
(b) Em nossa segunda alternativa primeiramente devemos encontrar a largura de pulso.
A largura do pulso é a distância que representa da amplitude do pulso, vamos observar a imagem exemplo e entender melhor:
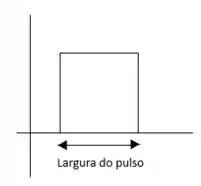
Não podemos esquecer que para encontrar a largura do pulso, devemos focar no eixo horizontal do gráfico beleza!
Focando nossos olhares para o gráfico observamos que a largura do pulso corresponde a subtração de:
Logo a largura de pulso é
Passo 3
(c) Devemos lembrar que a relação usada para calcular a frequência de repetição será:
Onde:
T corresponde ao período da onda.
Aplicando e substituindo os valores:
Quase acabamos, vamos para próxima alternativa!
Passo 4
(d) Antes de começamos vamos relembra como podemos encontrar o valor médio de uma onda pulsada. Para isso usaremos a relação:
Onde:
é a tensão do nível de base.
Memórias fresquinhas? Vamos colocar a mão na massa e resolver nosso item!
Para o ciclo de trabalho, que usaremos a equação descrita abaixo:
Ciclo de trabalho
Onde:
Corresponde a largura do pulso
T equivale ao período
Ciclo de trabalho
Ciclo de trabalho
Ciclo de trabalho Ciclo de trabalho
O próximo que devemos encontrar é o valor de pico, que corresponde a maior altura do pulso, que em nosso gráfico é .
E por fim ao observar o gráfico conseguimos observar a tensão de nível de base é .
Vamos agora substituir na equação do valor médio, beleza!
Passo 5
Ufa, essa é a última!
(e) Antes de começamos vamos relembra como podemos calcular o valor eficaz de uma onda pulsada na forma quadrangular, para isso utilizaremos a relação:
Vamos substituir em valores e encontrar o valor eficaz:
Resposta
(a)
(b) Largura de pulso é
(c)
(d)
(e)