O gráfico da corrente senoidal aparece na figura 13.90. Determine o tempo
Passo 1
Olá galera! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Bora começar então resolver nossa questão.
Primeiro Lembremos de forma sucinta o gráfico desta questão alternativa.
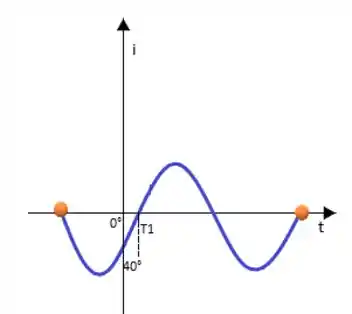
Desta corrente senoidal sabemos que a frequência angular será ω = 50000
Vou utilizar essa informação, para encontrar o período desta corrente:
Lembrando da fórmula teremos:
Isolando o Período
Substituindo os valores
Vamos terminar a questão no ´próximo passo?
Bora lá!
Passo 2
Agora estamos prontinhos para relacionar as grandezas.
A corrente senoidal está adiantada 40° ou seja, com relação a ela está adiantada 40°
Por que?
Porque (40 °-0°) = 40 °
Vamos fazer uma regrinha de três e encerra nosso exercício.
360 ° corresponde a 12,5 s que é o período da corrente, encontremos sua equivalência com 40°
Ângulo tempo
360°-------------12,5 x
40°---------------x
Aplicando meio por extremo, temos:
360 . X = 40 . 12 x
X =
Logo o = 1,388 x s
UFA! Acabou
Te vejo no próximo exercício.
Resposta
= 1,38 x s