A iluminação e os motores de uma pequena fábrica estabelecem uma demanda de potência igual a 10 kVA para um fator de potência atrasado de 0,7 com uma fonte de 208 V e 60 Hz.
a. Construa o triângulo de potência para a carga.
b. Determine o valor do capacitor que deve ser colocado em paralelo com a carga para elevar o fator de potência à unidade.
c. Determine a diferença entre as correntes da fonte no sistema não-compensado e no sistema compensado.
d. Repita os itens (b) e (c) para um fator de potência de 0,9.
Passo 1
Faaaaaala galerinha, tudo certo? Partiu resolver mais uma questãozinha!
Primeiramente, sabemos que um fator de potência 0,7 equivale a um ângulo de 45,573°. Tendo em vista isso, devemos agora encontrar as potências P e Q, para construirmos o triângulo de potências.
Do enunciado, temos que , portanto, para calcularmos P e Q, teremos:
Substituindo os valores na fórmula acima, temos:
Com os respectivos valores do ângulo e das potências, teremos o seguinte triângulo de potências:
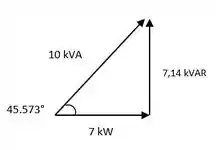
Passo 2
Para encontrarmos o valor C do capacitor, devemos primeiramente encontrar o valor de
Com o valor de encontrado, podemos substituí-lo na fórmula da capacitância de modo a encontrar o valor do capacitor que deve ser colocado em paralelo com a carga para elevar o fator de potência à unidade:
Passo 3
No sistema não-compensado, teremos:
No sistema compensado, teremos:
Portanto a diferença entre as correntes é:
Passo 4
Adotando a potência encontrada no item (a), quando o fator de potência for igual a 0,9, teremos:
Portanto:
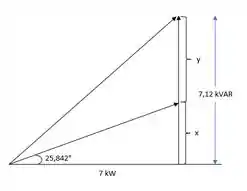
Para , o valor do capacitor que deve ser colocado em paralelo com a carga para elevar o fator de potência à unidade, será calculado da seguinte maneira:
No sistema não compensado teremos:
Enquanto no sistema compensado teremos:
Portanto a diferença entre as correntes é:
E é isso pessoal, finalizamos essa!!!! Vamos juntos resolver mais uma?
Resposta
a.
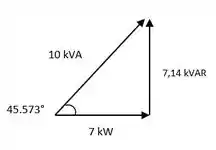
b. .
c.
d. e .