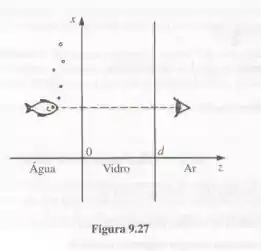
A luz de um aquário (Fig. 9.27) vai da água (n=34) através de um plano de vidro (n=23) no ar (n = 1). Assumindo que seja uma onda plana monocromática e que atinja o vidro com incidência normal, encontre os coeficientes de transmissão mínimo e máximo (Eq. 9.199). Você pode ver o peixe claramente.Com que nitidez ele pode ver você?
Passo 1
E ai meus amores nessa questãozinha “Pegue o que puder, sem nada a devolver” okay?

O índice de refração da água
O índice de refração do vidro
O índice de refração do ar é
Sabemos que o inverso do coeficiente de transmissão é
Passo 2
Então o coeficiente de transmissão
Para que o coeficiente de transmissão seja mínimo
Então
Para T ser máximo então
Então
Essa transmissão é boa (mais de 90%) para todas as frequências.
Quando trocamos e não há mudança é a equação do coeficiente de transmissão. Assim, fica claro que o peixe o vê tão bem quanto você o vê.
Depois dessa questão, “Ninguém se mexe” Meu cérebro caiu.”

Haha bora pra proximaaaa
Resposta
Resposta nos passos.