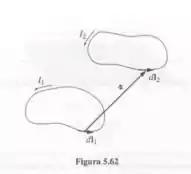
A magnetostática trata a 'corrente fonte' (a que estabelece o campo) e a corrente de prova' (a que sofre a força) tão assimetricamente que de forma alguma fica óbvio que a força magnética entre os dois circuitos de corrente é coerente com a terceira lei de Newton. Mostre, começando com a lei de Biot-Savart (5.32) e com a lei de força de Lorentz (5.16), que a força no circuito 2, devida ao circuito 1 (Figura 5.62), pode ser escrita como
Dessa forma, fica claro que F2 =-F1, já que muda de sentido quando os papéis de 1 e 2 são permutados. (Se parece que você está obtendo um termo 'a mais', vai ajudá-lo observar que .)
Passo 1
Olá pessoal, bora para mais uma!?
Podemos começar observando que pela lei de Biot-savart o campo no loop 1 pode ser da forma:
E a força no lool 2 pode ser expressa como:
Agora podemos rearranjar os produtos vetoriais utilizando a relação abaixo:
Com isso, temos que:
Rearranjando a expressão acima, temos que:
Passo 2
Repare que o primeiro termo é o que queremos encontrar, para isso o segundo deve ser nulo, então vamos investigar isso. Podemos começar expressando , assim temos:
Agora vamos pegar a expressão acima e encontra em relação ao ponto 2. Assim temos:
Derivando e melhorando um pouco a expressão acima, temos que:
Observe que se colocarmos 1/ em evidência, o termo de cima é , assim temos que:
Assim temos que:
Assim chegamos em:
Assim finalizamos mais uma questão! Até a próxima!
Resposta
Dedução nos passos 1 e 2.