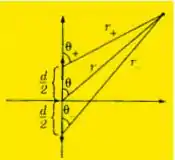
Como modelo de radiação quadrupolar elétrica, considere dois dipolos elétricos oscilantes com orientações opostas, separadas por uma distância , como mostra a Figura 11.10. Use os resultados da Seção 11.1.2 para os potenciais de cada dipolo, mas observe que eles não estão localizados na origem. Mantendo somente os termos de primeira ordem em :
(a) Encontre os potenciais escalar e vetorial.
(b) Encontre os campos magnético e elétrico.
(c) Encontre o vetor de Poynting e a potência radiada. Faça o gráfico do perfil de intensidade como função de .
Passo 1
Calma meu jovem, se você ficou com essa cara ao ler a questão
 ,
,
não se preocupe, chegaremos lá passo a passo. Vem comigo!!!
Na letra (a) a gente precisa encontrar os potenciais escalar e vetorial, então, temos o seguinte:
Temos que será
Onde .

Calma que vai dar certo! Hahaha
Na zona de radiação , o segundo termo é insignificante, então
Portanto,
Assim, na zona de radiação,

Calma, respira. Vamos para a letra (b).
Passo 2
Na letra (b) a gente tem que encontrar os campos magnético e elétrico. Vamos lá...
Para simplificar a notação, temos
Então,
na zona de radiação.
Na zona de radiação, temos:
Passo 3
(c)
Note que e
A integral é:
Assim, temos,
Note que ele vai como , enquanto a radiação do dipolo vai como .

Resposta
Ver Passos 1, 2 e 3.