Mostre que as series trigonométricas de Fourier para as funções dadas são como indicados. (Em todos os casos,)
Passo 1
Nessa questão ele pede para mostrar que as series trigonométricas de Fourier para as funções dadas são como indicados. (Em todos os casos,)


Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.
Passo 2
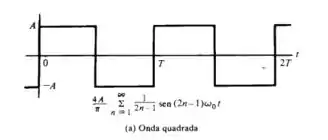
Na imagem (a),
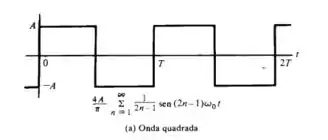
Série trigonométrica fica,
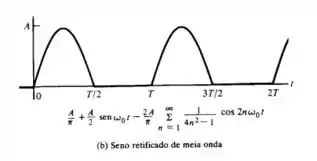
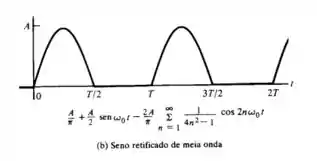
Na imagem (b) para,
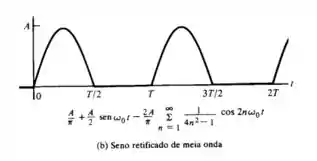
Passo 3
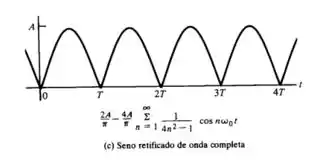
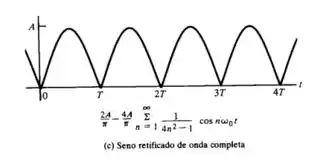
Na imagem ( c ) para,
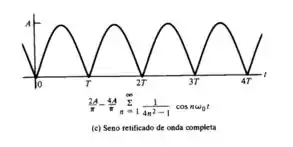
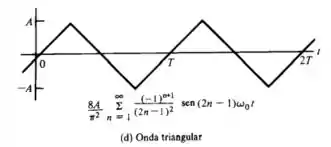
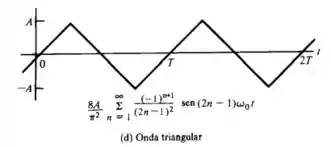
E por fim na imagem (d), tendo
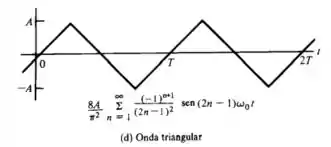
Temos,
Espero ter ajudado, até próxima.

Resposta
a)
b)
c)
d)