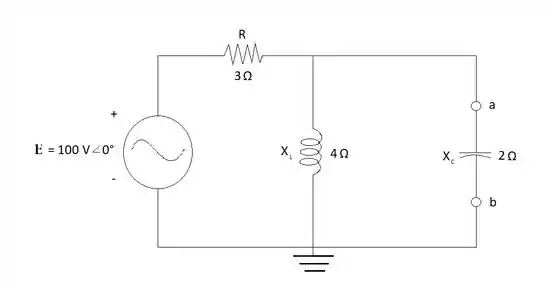
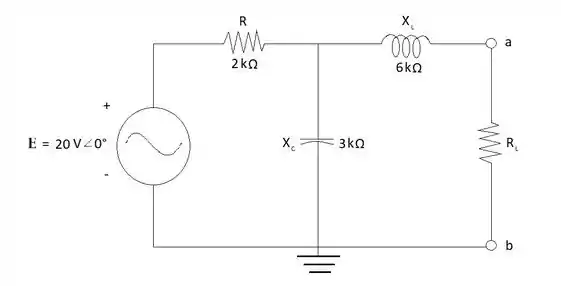
Obtenha o circuito equivalente de Norton para o circuito externo aos elementos entre a e b para os circuitos mostrados na figura 18.120
Passo 1
Para encontrar o circuito equivalente de Norton do primeiro circuito primeiro se redesenha o circuito sem a parte do capacitor e se realiza o cálculo da impedância equivalente desconsiderando a presença da fonte de tensão:
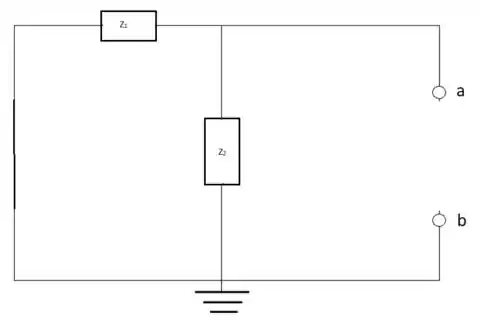
ZN = Z1Z2 = = 2,4 Ω 36,87°
Para encontrar o valor da corrente de Norton se substitui a parte onde estava o capacitor por um fio que acaba provocando um curto-circuito na impedância do indutor, logo a corrente no indutor é de 0A.
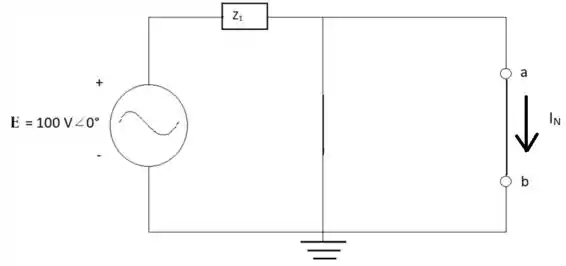
Dessa forma se tem apenas uma fonte de tensão que é a tensão que será usada para o cálculo da corrente de Norton com a respectiva impedância do resistor que sobrou logo após o curto-circuito:
IN = E/Z1 = = 33,33 A 0°
Passo 2
Para o seguinte circuito se realiza o mesmo processo em relação ao desenho do circuito anterior, mas desta vez é o RL que deve ser retirado:
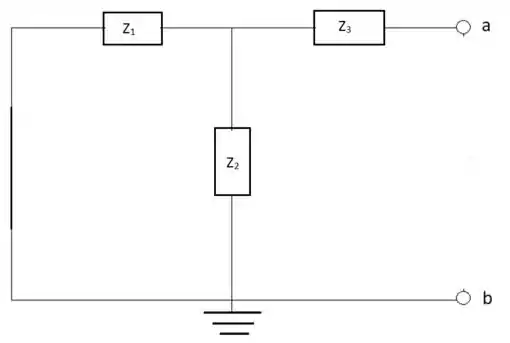
ZN = Z1Z2 + Z3 = 5,26 Ω74,74°
Em relação a encontrar a corrente que passa pelo circuito se substitui a resistência RL por um curto-circuito. Após isso se realiza o cálculo da corrente:
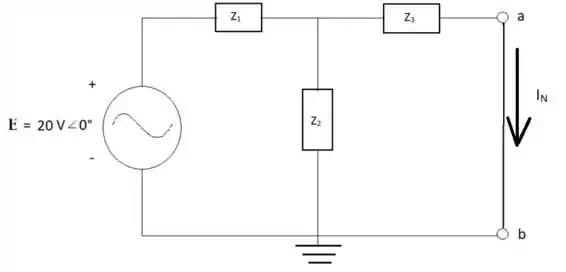
Z = Z2Z3 = -j6
E’ =
IN = E’/Z3 = = 3,16 mA-108,43°
Resposta
- ZN = 2,4 Ω 36,87°
- ZN = 5,26 Ω 74,74°
IN = 33,33 A 0°
IN = 3,16 mA 108,43°