Obtenha o circuito equivalente de Norton para o circuito externo aos elementos entre a e b para os circuitos vistos na Figura 18.122.
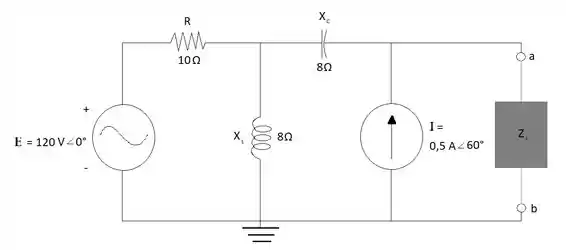
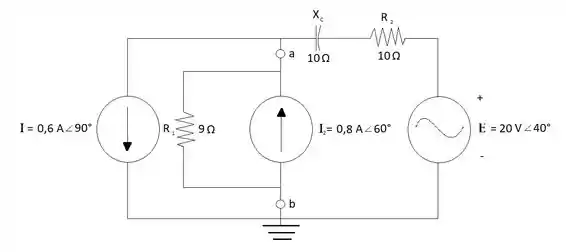
Passo 1
Para encontrar o circuito equivalente de Norton para o primeiro circuito devemos encontrar a impedância ZN e a corrente IN. Para isso, primeiro devemos retirar a impedância ZL do circuito e substituir as fontes de tensão e corrente por um curto-circuito e um curto-circuito aberto, respectivamente:
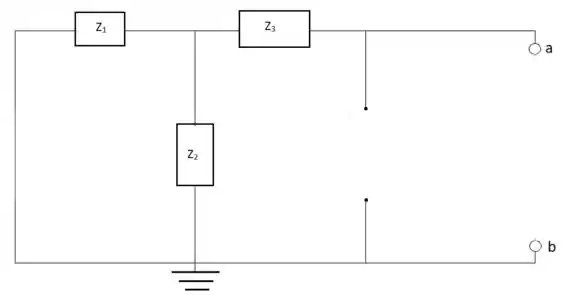
ZN = Z3 + Z1Z2 = = 4,9976 Ω-38,6598°
Para encontrar a corrente IN é necessário substituir a impedância ZL por um curto-circuito e calcular a corrente que passa pelo mesmo aplicando análise de malhas:
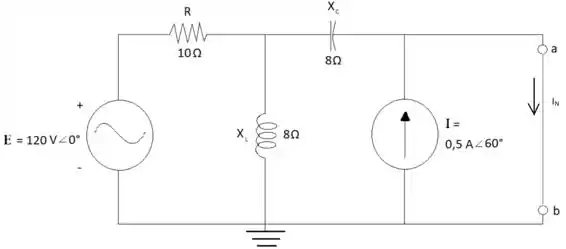
I3 – I2 = 0,5 A0°
10I1 + j8(I1 - I2) = 120 V0°
j8(I2 – I1) – j8(I2) = 0
Resolvendo esse sistema obtemos o seguinte valor para IN:
IN = I3 = 15,44 A89,07°
Passo 2
Para encontrar o circuito de Norton do segundo circuito se aplica o mesmo processo feito no circuito anterior, começando com encontrar a impedância de Norton retirando-se do circuito a fonte de corrente I2 e o resistor R1:
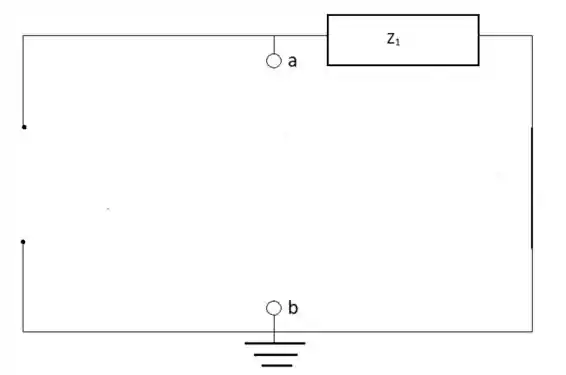
Z1 = ZN = 10 – j10 = 14,14 Ω-45°
Para encontrar a corrente IN se substitui a fonte de corrente I2 e o resistor R1 por um curto-circuito e se aplica análise de malhas para descobrir qual é a corrente que passa por ela:
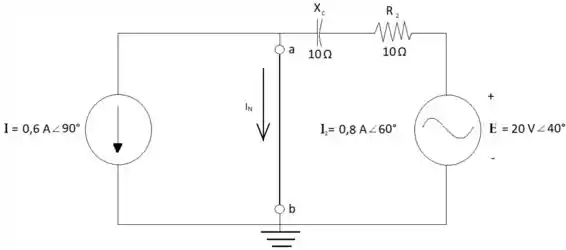
Ia = -0,6 A90°
-j10(Ib) + 10(Ib) = -2040°
Se resolve essa equação para encontrar o valor de Ib. Podemos escrever o valor da corrente de IN da seguinte forma:
IN = Ia – Ib = 0,82 A81,34°
Resposta
- ZN = 4,9976 Ω-38,6598°
- ZN = 14,14 Ω-45°
IN = 15,44 A89,07°
IN = 0,82 A81,34°