Obtenha o circuito equivalente de Norton para o circuito externo à fonte de corrente , visto na Figura 18.118.
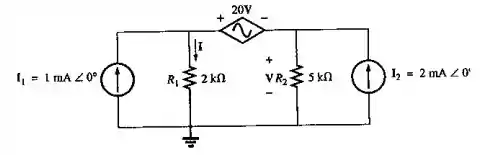
Passo 1
Oiii, gente! Tudo bem? Bora para mais um exercício de circuitos!
Primeiro, vamos listar as impedâncias do circuito. Podemos ignorar o resistor de pois estamos interessados no circuito externo ao mesmo.
Show! Vamos então descobrir os valores de corrente e impedância equivalentes de Norton para este circuito.
Passo 2
Iremos partir do equivalente de Thévenin para chegar no de Norton. Para isso, devemos substituir por um circuito aberto e analisar seus terminais.
Primeiramente, note que a tensão de Thévenin é a mesma sobre . Chamando esta tensão de , temos que:
Logo, precisamos determinar ainda a variável V. Para isso, veja que a corrente da fonte se divide em duas correntes:, para impedância (como indicado na imagem) e , para impedância . Logo:
Pela lei de Ohm, temos na impedância :
Assim, obtemos:
Passo 3
Em seguida, vamos calcular a corrente equivalente de Norton. Para isso, devemos substituir por um curto circuito e determinar a corrente que passa por ele.
Observe que, nesse caso, nenhuma corrente irá passar pela impedância , pois a corrente sempre busca o caminho de menor resistência (o curto circuito). Com isso, a fonte de tensão e ficam em paralelo, ou seja, a tensão sobre a impedância deve ser de (igual à da fonte). Como para todo , a tensão é nula nestes dois elementos. Portanto, a corrente equivalente de Norton é igual a .
Pela Lei de Ohm: