a. Obtenha o circuito equivalente de Norton para o circuito externo à reatância indutiva de 4 kΩ visto na Figura 18.115.
Passo 1
Falaa galerinhaa!!! Tudo certinhoo?? Bora juntos pra mais uma!!
Aqui, nós temos que
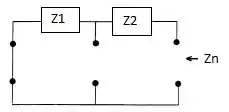
Vamos organizar Z1, Z2 e Z3. Pelo circuito da Figura 18.123, tendo que
Assim, temos que encontrar Zn, tendo que Z1 e Z2 estão em série, ou seja, temos que:
Logo, temos que, substituindo pelos valores,
Passo 2
Agora, precisamos encontrar as correntes nesse circuito. Antes disso, observando o circuito, podemos perceber que há divisão de corrente, tendo I1 e I2 somadas. Assim, temos que encontrar as duas correntes, tendo que:
Já para I2, temos:
Agora, finalmente, conseguimos encontrar a corrente de Norton, tendo que: