a. Obtenha o circuito equivalente de Norton para o circuito externo à reatância indutiva de 5 kΩ visto na Figura 18.123.
Passo 1
Falaa galerinhaa!!! Tudo certinhoo?? Bora juntos pra mais uma!!
Aqui, nós temos que
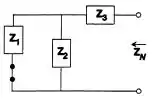
Vamos organizar Z1, Z2 e Z3. Pelo circuito da Figura 18.123, tendo que
Assim, temos que encontrar Zn, tendo que Z1 e Z2 estão em paralelo, e Z2 e Z3 estão em série, ou seja, temos que:
Substituindo os valores, temos:
Passo 2
Agora, vamos calcular V2, tendo que:
Substituindo os valores que temos, ficamos com:
Resolvendo essas contas, temos que:
Calma, estamos acabando!! Agora, finalmente, conseguimos encontrar In, tendo que:
Prontinho, fizemos o circuito de Norton para o circuito externo ao capacitor da Figura 18.113.
É isso, galerinhaaa!! Até a próxima