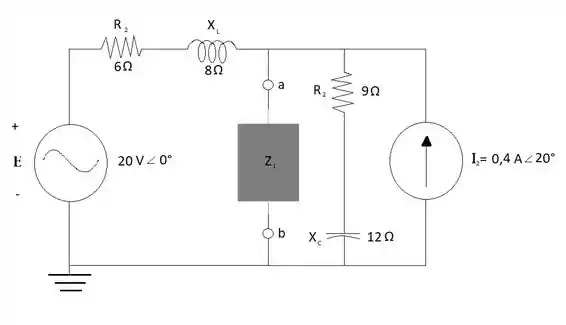
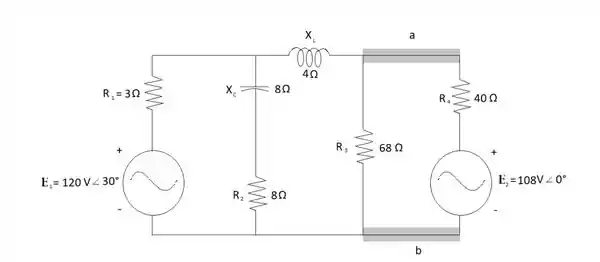
Obtenha o circuito equivalente de Norton para as partes dos circuitos vistos na Figura 18.126 externas aos elementos entre os pontos a e b.
Passo 1
Para encontrar a impedância de Norton do primeiro circuito precisamos retirar a impedância ZL, a fonte de tensão deve ser substituída por um curto-circuito e a fonte de corrente deve ser substituída por um curto-circuito aberto:
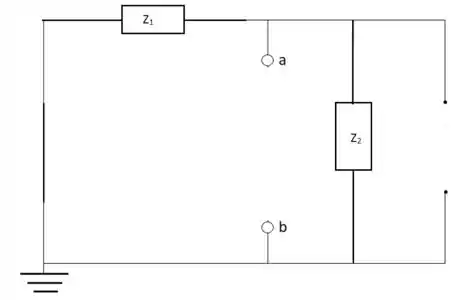
ZN = Z1 Z2 = 9,66 Ω14,93°
Para encontrar a corrente IN devemos substituir a impedância ZL por um curto-circuito e aplicar análise malhas:
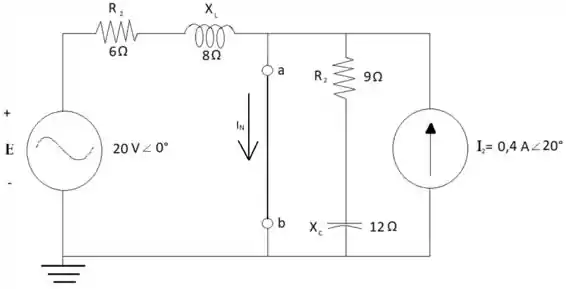
6(I1) +j8(I1) = 200°
I2 = -0,420°
9(I3 – I2) – j12(I3 – I2) = 0
Resolvendo esse sistema podemos calcular a corrente IN que se dá pela expressão:
IN = I1 – I3 = 2,15 A-42,87°
Passo 2
Para encontrar a impedância de Norton do segundo circuito é preciso retirar toda a malha que engloba os resistores R3, R4 e também a fonte de tensão E2:
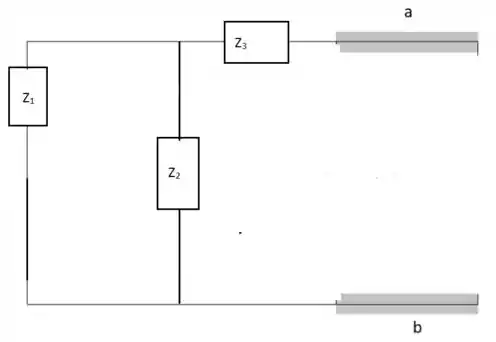
ZN = Z3 + Z1Z2 = 4,37 Ω55,68°
Para encontrar o valor da corrente IN se substitui toda a malha mencionada anteriormente por um curto-circuito, encontramos a corrente que percorre o circuito todo e em seguida aplicamos a fórmula de divisor de corrente:
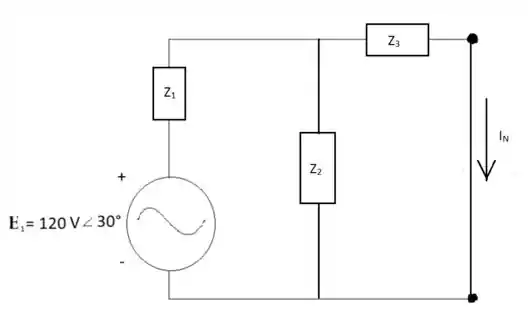
I = E1/ZT = = 18,05 A-16,22°
IN = Z2(I)/(Z2 + Z3) = = 22,83 A-34,65°
Resposta
- ZN = 9,66 Ω14,93°
- ZN = 4,37 Ω55,68°
IN = 2,15 A-42,87°
IN = 22,83 A-34,65°