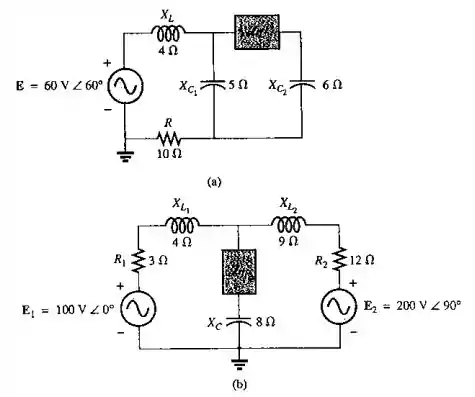
Obtenha a impedância da carga para os circuitos vistos na Figura 18.129 de maneira que a potência fornecida à carga seja máxima e calcule o valor dessa potência.
Passo 1
Oiee, pessoal, de boa? Bora para mais um exercício de circuitos!
Primeiro, vamos lembrar que a máxima transferência de potência para carga ocorre quando , isto é, devemos obter o circuito equivalente de Thévenin para o circuito externo à carga .
Iremos começar pelo item (a), beleza? Vamos listar as impedâncias desse circuito.
Passo 2
Desligando a fonte , obtemos um curto circuito em seu lugar, de modo que e ficam em série:
Esta associação entre e fica em paralelo com :
Passo 3
Por fim, temos uma última associação em série. Logo, é dado por:
Assim, e
Para determinar , devemos substituir a carga por um circuito aberto e analisar os terminais. Com isso, vemos que é igual a tensão sobre (a corrente em é nula). Logo, podemos calcular o divisor de tensão:
Portanto, a potência máxima fornecida à carga é de:
Passo 4
Em seguida, podemos ir para o item (b). Vamos listar as impedâncias desse circuito. Como e estão em série, assim como e , iremos considerar a impedância resultante destas associações.
Desligando as fonte e , obtemos um curto circuito em seus lugares, de modo que e ficam em paralelo, e esta associação fica em série com . Logo, é dado por:
Assim, e
Passo 5
Para determinar , iremos substituir a carga por um circuito aberto e analisar seus terminais. Assim, obtemos o seguinte circuito equivalente:
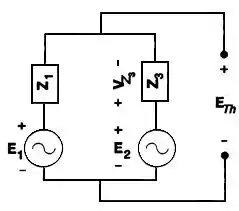
Note que omitimos pois nenhuma corrente passa por ela, graças a inserção de um circuito aberto associado em série com esta impedância. Na malha da esquerda, temos, pela LKT:
Passo 6
Como , ficamos com:
Já na malha da direita, temos:
Portanto, a potência máxima fornecida à carga é de:
Resposta
a. e
b. e