Permute os Rs e Cs no circuito da Figura P15.48; isto é, substitua por por por por e por
a) Descreva o tipo de filtro implementado como resultado da permuta.
b) Confirme o tipo de filtro descrito em (a) deduzindo sua função de transferência . Escreva a função de transferència na forma que a torne compativel com a Tabela 15.1.
c) Faça calcule as expressões para , e em termos de e . (Veja o Problema para a definição de e
d) Suponha que o filtro descrito em (a) seja usado no mesmo tipo de filtro Butterworth de terceira ordem que tem um ganho na faixa de passagem de 8. Com , calcule os valores de , e na seção de segunda ordem do filtro.
Passo 1
Para frequências muito pequenas, os capacitores se comportam como circuitos abertos e, portanto, v0 é zero. À medida que a frequência aumenta, as impedâncias capacitivas do ramo tornam-se pequenas em comparação com os ramos resistivos. Quando isso acontece que o circuito se torna um amplificador inversor com o capacitor dominando o caminho de realimentação. Assim, o ganho do amplificador se aproxima de ou . Portanto, o circuito se comporta como um filtro passa-altas com ganho de banda passante de.
[a] Por hipótese, o circuito se torna:
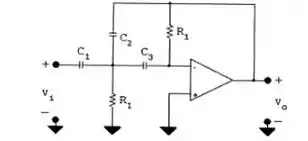
Passo 2
[b] Somando as correntes longe do terminal superior de rende
ou
A soma das correntes do terminal de entrada inversora fornece
ou
Portanto podemos escrever
Resolvendo para
Portanto, o circuito implementa um filtro passa-altas de segunda ordem com ganho de banda passante de .
Passo 3
Passo 4
[d] Da Tabela 15.1, a função de transferência da seção de segunda ordem de um filtro Butterworth passa-alta de terceira ordem é
Portanto Então
Resposta
a. Portanto, o circuito se comporta como um filtro passa-altas com ganho de banda passante de.
b. Portanto, o circuito implementa um filtro passa-altas de segunda ordem com ganho de banda passante de .
c.
d.