Permute os Rs e Cs no circuito da Figura P15.53, isto é, substitua por por e vice-versa.
a) Analise o circuito do ponto de vista qualitativo preveja o tipo de filtro implementado pelo circuito.
b) Verifique a conclusão a que chegou em (a) deduzindo a função de transferência . Escreva a função de transferência de uma forma que a torne compatível com a Tabela 15.1.
c) Quantas escolhas livres há na seleção dos componentes do circuito?
d) Determine e em função de e .
e) Há alguma restrição para e ?
f) Suponha que o circuito seja usado em um filtro Butterworth passa-baixas de terceira ordem do tipo determinado em (a). Especifique os valores de e na seçāo de segunda ordem do filtro protótipo se .
Passo 1
[a] A troca de R s e C s resulta no seguinte circuito.
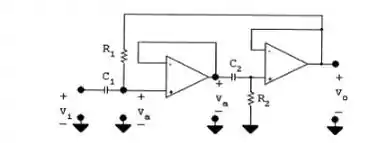
Em baixas frequências, os capacitores aparecem como circuitos abertos e, portanto, a tensão de saída é zero. À medida que a frequência aumenta, as ramificações do capacitor aproximam-se dos curtos-circuitos e . Assim, o circuito é um filtro passa-alta de ganho unitário.
Passo 2
[b] As equações do domínio s são
Segue que
E
Por isso
Passo 3
[c] Existem 4 componentes do circuito:. Existem duas restrições de função de transferência: e . Portanto, há duas escolhas livres.
Passo 4
Passo 5
[e] Não, todos os capacitores realizáveis produzirão resistores realizáveis.
Passo 6
[f] A seção de segunda ordem em um filtro passa-alta Butterworth de 3ª ordem é
Portanto e
Resposta
a. o circuito é um filtro passa-alta de ganho unitário.
b.
c. há duas escolhas livres.
d.
e. Não, todos os capacitores realizáveis produzirão resistores realizáveis.
f.