Projete um circuito ressonante em série com uma tensão de entrada de e as seguintes especificações:
a. Uma corrente máxima de 500 mA na ressonância.
b. Uma largura de banda de 120 Hz.
c. Uma frequência de ressonância de 8400 Hz.
Determine os valores de L e C e as frequências de corte.
Passo 1
Fala fala meu povo, tudo certo? Bora lá resolver mais essa questão juntos!!
Através das especificações dadas no enunciado, podemos projetar o seguinte circuito:
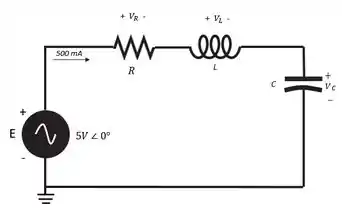
Passo 2
Com a projeção do circuito e os valores da largura de banda e da frequência de ressonância dadas no enunciado, notamos que para encontrar os valores de L e C, devemos primeiramente encontrar o valor de R, a partir da seguinte fórmula:
Com os valores de E e dados no enunciado, substituiremos na fórmula acima:
Passo 3
Em seguida, devemos encontrar o valor de através da fórmula de largura de banda:
Substituindo os valores da frequência e da largura de banda dadas no enunciado, teremos:
Passo 4
Com o valor de encontrado no passo anterior, calcularemos os valores de para então encontrarmos o valor de L e C.
Como o circuito ressonante está em série, podemos afirmar que: . Além disso, sabemos que o fator de qualidade () é dado por:
.
Sendo assim, substituiremos os valores encontrados nos passos anteriores para achar os valores de :
Passo 5
Para encontrarmos o valor de L, sabemos que a fórmula de L é dada por: , e utilizando os dados fornecidos no enunciado para a frequência e o valor de encontrado no passo anterior, temos que:
Para encontrarmos o valor de C, sabemos que a sua fórmula é dada por: , e utilizando os dados fornecidos no enunciado para a frequência e o valor de encontrado no passo anterior, temos que:
Passo 6
Finalmente, sabemos que as frequências de corte f1 e f2 podem ser determinadas a partir do valor da largura de banda, bem como da frequência . Sendo assim, temos:
e .
Portanto:
Resposta
a.
b. , , e .