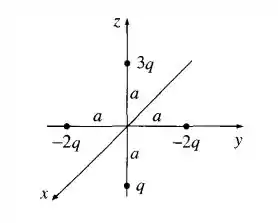
Quatro partículas (uma de carga q. uma de carga e duas de carga ) estão dispostas como mostra a Figura 3.31. cada uma delas a uma distância da origem. Encontre uma fórmula simples aproximada para o potencial, válida em pontos distantes da origem. (Expresse sua resposta em coordenadas esféricas.)
Passo 1
Faaaaala meu povo, bora iniciar mais uma questãozinha do nosso livro!
Para iniciarmos nosso problema iremos analisar a imagem abaixo, note que temos 4 cargas de magnitude , , e nas posições , , e , respectivamente.
Como a carga total da distribuição é zero, o primeiro termo dominante, se não desaparecer, é o termo dipolo:
Tudo certinho, até aqui? Vamos seguir!
Passo 2
Iremos agora calcular o momento dipolo a partir da equação:
Onde:
Com isso a gente pode seguir para nosso último passo!
Passo 3
A partir da equação:
As grandes distâncias da origem, o potencial da distribuição dada pode ser aproximado por:
Dessa forma, chegamos ao seguinte resultado:
Tranquilão? Te vejo na próxima!