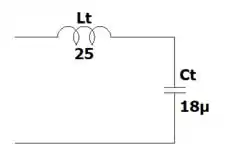
Reduza os circuitos da figura 12.86 ao menor número possível de elementos
Passo 1
Oieee, tudo certo?
Primeiro vamos lembrar que a indutância equivalente funciona igual com resistores, se for em série fica:
E se for em paralelo:
Pra capacitância é ao contrário, em série é assim:
E em paralelo:
Agora vamos lááá
Passo 2
a) Primeiro temos esse circuito
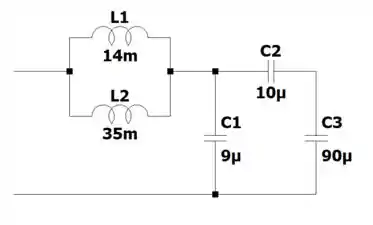
A indutância equivalente é dada por em paralelo com :
Agora para a capacitância
Vamos calcular a capacitância , que é a associação em série de com
Por fim, a capacitância equivalente vai ser em paralelo com :
Então, o nosso circuito fica assim:
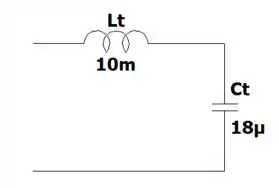
Passo 3
b) Agora vamos para esse circuito
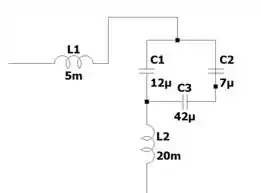
A capacitância equivalente é dada por em série com e tudo isso em paralelo com :
E a indutância equivalente, depois que a capacitância já foi ajustada, vai ser em série com
Então, o circuito fica assim
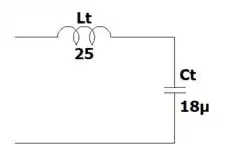
Resposta
a) 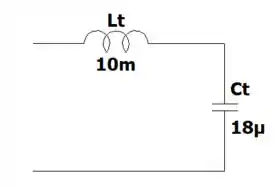
b)