Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku, Elementos de Eletromagnetismo- Ed: 5º - Capítulo 2.Questões de Revisão - Ex. 9

Relacione os itens da coluna da esquerda com os da coluna da direita. Cada resposta pode ser usada uma vez, mais de uma vez ou em nenhuma vez.

  1. θ = π / 4  
  2. ϕ = 2 π / 3
  3. x = - 10
  4. r = 1 ,   θ = π / 3 , ϕ = π / 2
  5. ρ = 5
  6. ρ = 3 ,   ϕ = 5 π / 3
  7. ρ = 10 ,     z = 1
  8. r = 4 ,   ϕ = π / 6
  9. r = 5 ,   θ = π / 3

(i) plano infinito

(ii) semipleno infinito

(iii) círculo

(iv) semicírculo

(v) linha reta

(vi) cone

(vii) cilindro

(viii) esfera

(ix) cubo

(x) ponto

Passo 1

  1. θ = π 4

    2. Partindo de θ = c o n s t a n t e do sistema de coordenadas esféricas é um cone circular com o eixo de z.

    Portanto, um cone é formado em θ = π / 4 .

    Passo 2

  2. ϕ = 2 π / 3

    3. Considerando um sistema de coordenadas cilíndricas.

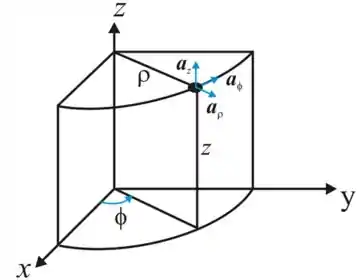
    Do sistema de coordenadas cilíndricas ϕ = c o n s t a n t e   e   s e m i p l a n o   i n f i n i t o .

    Portanto, um plano semi-infinito é formado por ϕ = 2 π / 3

    Passo 3

  3. x = - 10

    4. Em constante x, chance da 1ª ,2ª ,3ª ,4ª coordenadas na coordenada cartesiana, com as variáveis x, y, e z, serão:

    - 10 , y , z , - 10 - y , z , - 10 , y , - z , - 10 , - y , - z

    Consequentemente o plano será infinito.

    Passo 4

  4. r = 1 ,   θ = π / 3 , ϕ = π / 2

    5. Do sistema de coordenadas esféricas r = c o n s t a n t e é uma esfera de raio r com seu centro na origem ; θ = c o n s t a n t e é um cone circular com o eixo z como seu eixo e a origem como seu vértice; ϕ = c o n s t a n t e   é o plano semi-infinito como no sistema cilíndrico. Um ponto é uma interseção das três superfícies, logo

    r = 1 ,   θ = π / 3 = ϕ = π / 2 é o ponto ( 1 ,   π / 3 , π / 2 )

    Passo 5

  5. ρ = 5

    6. Onde o sistema de coordenadas cilíndricas , ρ = c o n s t a n t e é um cilindro circular.

    Um cilindro circular é formado em ρ = 5 .

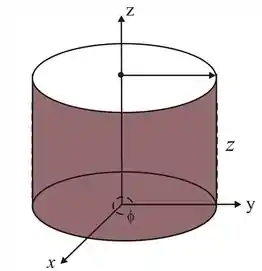
    Passo 6

  6. ρ = 3 ,   ϕ = 5 π / 3

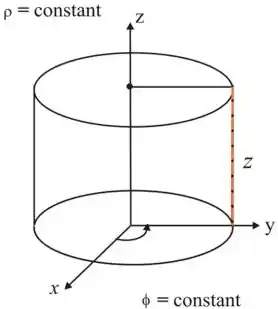
    7. Do sistema de coordenadas cilíndricas, o ρ = r a i o   d o   c i l i n d r o   e   ϕ = c o n s t a n t e é o plano semi-infinito; Uma linha reta é formada pela interseção de duas superfícies.

    Passo 7

  7. ρ = 10 ,     z = 1

    8. Partindo do sistema de coordenadas cilíndricas, ρ = r a i o   d o   c i l i n d r o   e   z = c o n s t a n t e , um círculo é formado pela interseção de duas superfícies.

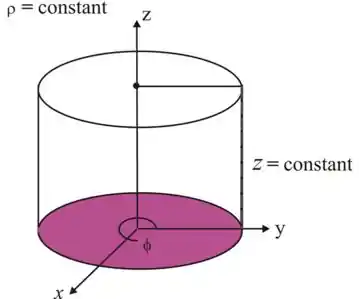
    Passo 8

  8. r = 4 ,   ϕ = π / 6

    9. Do sistema de coordenadas esféricas, r = c o n s t a n t e é uma esfera de raio r com seu centro na origem; ϕ = c o n s t a n t e é o plano semi-infinito como no sistema cilíndrico. Um semicírculo é uma interseção das duas superfícies.

    Passo 9

  9. r = 5 ,   θ = π / 3

Do sistema de coordenadas esféricas r = c o n s t a n t e é uma esfera de raio r com seu centro na origem; θ = c o n s t a n t e é um cone circular com o eixo z como seu eixo e a origem como seu vértice; um círculo é uma interseção das duas superfícies.

Passo 2

Mediante as explicações que foram mencionadas acima, podemos concluir e combinar da seguinte maneira

  1. → (vi)
  2. →   (ii)
  3. → (i)
  4. →   (x)
  5. → (vii)
  6. → (v)
  7. →   (iii)
  8. → (iv)
  9. → (iii)

Resposta

Veja o passo a passo.