Repita o problema se é a função do exercício
Passo 1
Nessa questão ele pede para calcular a resposta foçada no circuito da figura , se é a função do problema , com .
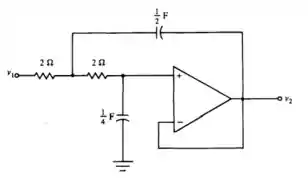
Se é,
Com .

Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.
Passo 2
Sabendo que,
Com .
Lembrando que para série de Fourier trigonométrica, temos
Ficando,
Espero ter ajudado, até próxima.

Resposta