22. Repita o problema 21 para uma capacitância de .
a) Determine a constante de tempo do circuito quando a chave é colocada na posição 1.
b) Determine a expressão matemática para tensão entre os terminais do capacitor após a chave ter sido colocada na posição 1.
c) Determine a expressão matemática para a corrente depois que a chave é fechada (posição 1).
d)Determine a tensão e a corrente se a chave é colocada na posição 2 em
e) Determine as expressões matemáticas para tensão e a corrente se a chave for colocada na posição 3 em .
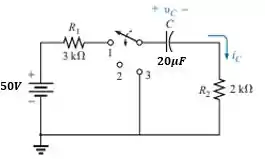
Figura 10.84- com a alteração no valor da capacitância
Passo 1

Para a felicidade de todos, temos um circuito praticamente igual ao do problema anterior 😊, diferente apenas nos valores numéricos das grandezas.
Por isso, basta seguir os mesmos passos!
Vamos anotar as informações do problema:
Passo 2
a) Calcular a constante de tempo através da relação:
Como há dois resistores neste circuito, temos que calcular a resistência equivalente.
Passo 3
Agora podemos calcular a constante de tempo:
Passo 4
b) Agora vamos encontrar a expressão matemática para a tensão para a constante de tempo de terminada no item anterior. A expressão geral para é dada por:
Agora, basta inserir as informações que temos sobre o problema, assim chegamos à:
Passo 5
c) Determine a expressão matemática para a corrente quando a chave estiver na posição 1. Vamos partir da expressão geral da corrente, representada por:
Agora vamos inserir as informações que temos até o momento, assim:
Passo 6
d) Determine a tensão e a corrente se a chave é colocada na posição 2 em . Para o tempo proposto, temos a exponencial descrita por:
Desta forma, temos:
Passo 7
Ainda no item d- utilizaremos o valor encontrado para exponencial, para determinar a tensão e a corrente .
Agora, para a corrente, temos a expressão:
Passo 8
e) Determine as expressões matemáticas para tensão e a corrente se a chave for colocada na posição 3 em . Para isso, teremos que calcular a constante de tempo para essa nova configuração de circuito.
Agora basta inserir o novo valor da constante de tempo, nas equações já trabalhadas nos itens b e c. Sendo assim, temos a tensão:
V
Para a corrente, há considerações a serem feitas: o sentido da corrente se inverte, logo, haverá um sinal contrário para a corrente, expressa por:
Passo 9
Ainda no item e – Vamos inserir nas equações da corrente e da tensão a informação do intervalo de tempo . Assim obtemos:
Passo 10
f) Trace as formas de e para o intervalo de até .
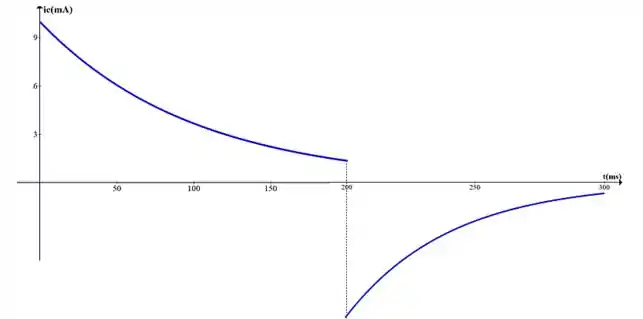
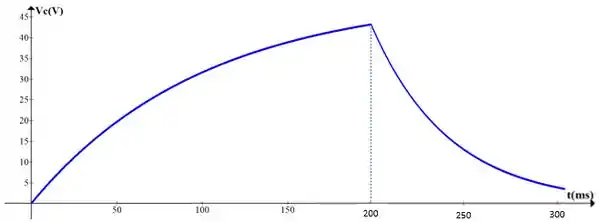
Resposta
a)
b)
c)
d) ;
e)