Repita o Problema 15 para uma carga capacitiva com uma reatância de 20 ohms.
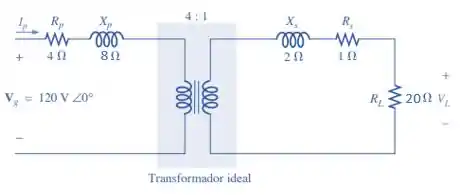
Figura 21.59
Passo 1
Olá galera!
Mais um probleminha que irá utilizar as informações da Figura 21.59. Mas, neste caso a carga resistiva será substituída por uma carga capacitiva, diferente do problema 15. Essa alteração não interfere nos valores de , por conta disso, podemos trabalhar com os valores encontrados no problema 14.
a) Sendo assim, a impedância total, será expressa por:
Com as informações em mãos, teremos:
Passo 2
b) Da mesma forma que fizemos no problema anterior, a corrente será calculada por:
Isso nos leva à:
Passo 3
c) As tensões serão expressas como:
E,
Passo 4
d) Nos itens anteriores, já calculamos os módulos e direções, agora é só montar o diagrama:
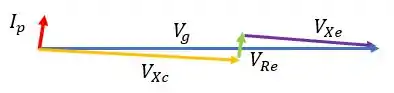
Resposta
a) ; b) ; c) , ,